Question
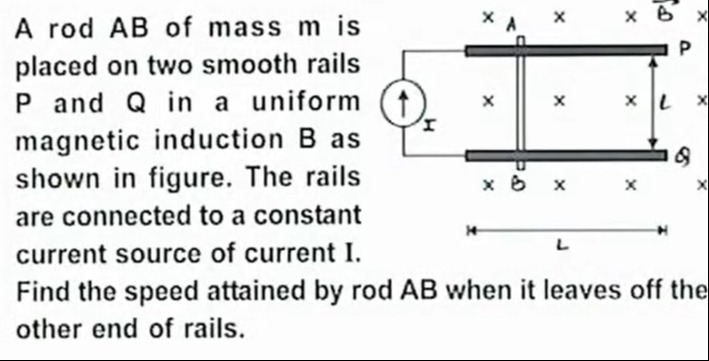
Question: A rod AB of mass m is placed on two smooth rails P and Q in a uniform magnetic induction B as shown ...
A rod AB of mass m is placed on two smooth rails P and Q in a uniform magnetic induction B as shown in figure. The rails are connected to a constant current source of current I. Find the speed attained by rod AB when it leaves off the other end of rails.
ℓm2IB
Solution
The magnetic force on the rod is given by F=IℓB, where ℓ is the length of the rod (distance between the rails). This force is constant since I, ℓ, and B are constant. The rod starts from rest and moves a distance ℓ along the rails. Using the work-energy theorem, the work done by the magnetic force is converted into kinetic energy. Work done W=F×ℓ=(IℓB)×ℓ=Iℓ2B. The kinetic energy of the rod is KE=21mv2. Equating work done to kinetic energy: 21mv2=Iℓ2B. Solving for v, we get v=m2Iℓ2B=ℓm2IB.
