Question

A rocket is launched normal to the surface of the Earth, away from the sun, along the line joining the Sun and the Earth. The Sun is $3\times {{10}^{5}}$ times heavier than the Earth and is at a distance $2.5\times {{10}^{4}}$ times larger than the radius of the Earth. The escape velocity from Earth’s gravitational field is ${{v}_{e}}=11.2\,\,km{{s}^{-1}}$. The minimum initial velocity $({{v}_{s}})$ required for the rocket to be able to leave the Sun-Earth system is closest to (Ignore the rotation and revolution of the Earth and the presence of any other planet)
(A) ${{v}_{s}}=62\,\,km{{s}^{-1}}$
(B) ${{v}_{s}}=42\,\,km{{s}^{-1}}$
(C) ${{v}_{s}}=72\,\,km{{s}^{-1}}$
(D) ${{v}_{s}}=22\,\,km{{s}^{-1}}$

Answer 1

To find the minimum initial velocity, we use conservation of energy theorem. From law of conservation of energy, we have
Loss in kinetic energy = Gain in potential energy

Complete step by step solution:
Let ${{M}_{e}}$ be the mass of Earth and $R$ be the radius of Earth.
Given: Mass of Sun ${{M}_{s}}=3\times {{10}^{5}}{{M}_{e}}$, Distance between Earth and Sun $d=2.5\times {{10}^{4}}R$, Escape velocity ${{v}_{e}}=11.2\,\,km{{s}^{-1}}$

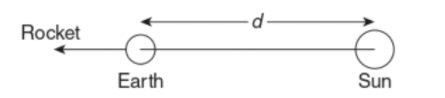
According to law of conservation of energy, we get
$\dfrac{1}{2}m{{v}_{s}}^{2}=\dfrac{G{{M}_{e}}m}{R}+\dfrac{G{{M}_{s}}m}{R+d}$ $...(\text{i})$
Where $m$ is the mass of the rocket.
But here $d>>R$, so we can write $R+d\approx d$
By putting the given values in equation $(\text{i})$, we get
$\Rightarrow \dfrac{1}{2}m{{v}_{s}}^{2}=\dfrac{G{{M}_{e}}m}{R}+\dfrac{G(3.5\times {{10}^{5}}{{M}_{e}})m}{2.5\times {{10}^{4}}R}$
$\Rightarrow \dfrac{1}{2}m{{v}_{s}}^{2}=\dfrac{G{{M}_{e}}m}{R}\left( 1+\dfrac{3\times {{10}^{5}}}{2.5\times {{10}^{4}}} \right)$
$\Rightarrow \dfrac{1}{2}m{{v}_{s}}^{2}=\dfrac{G{{M}_{e}}m}{R}\left( 1+12 \right)$
$\Rightarrow \dfrac{1}{2}m{{v}_{s}}^{2}=\dfrac{13G{{M}_{e}}m}{R}$
$\Rightarrow {{v}_{s}}^{2}=2\times \dfrac{13G{{M}_{e}}}{R}$
$\Rightarrow {{v}_{s}}=\sqrt{2\times \dfrac{13G{{M}_{e}}}{R}}$ $...(\text{ii})$
It is given that escape velocity ${{v}_{e}}=11.2\,\,km{{s}^{-1}}$.
Escape velocity on earth is defined as the minimum velocity with which the body has to be projected vertically upwards from the surface of earth so that it crosses the gravitational field of earth and never returns.
Escape velocity of Earth is given by,
${{v}_{e}}=\sqrt{\dfrac{2G{{M}_{e}}}{R}}$ $...\text{(iii)}$
Where $G=$ universal gravitational constant. Its value is $6.67\times {{10}^{-11\,\,}}{{m}^{3}}k{{g}^{-1}}{{s}^{-2}}$
Put the value of equation $(\text{iii})$ in equation $(\text{ii})$, we get
${{v}_{s}}=\sqrt{13}\,{{v}_{e}}$
$\Rightarrow {{v}_{s}}=\sqrt{13}\times 11.2$
$\Rightarrow {{v}_{s}}=40.38\,\,km{{s}^{-1}}$
$\Rightarrow {{v}_{s}}\approx 42\,\,km{{s}^{-1}}$

Note: Escape velocity is the minimum velocity with which the body must be thrown so that it just escapes the gravitational field of the nearby object. Here in our case a nearby object is Earth and sun.