Question

A rocket is fired vertically from the earth with an acceleration of $2\;g$, where $g$ is the gravitational acceleration. On an inclined plane inside the rocket, making an angle $\theta$ with the horizontal, a point object if mass $m$ is kept. The minimum coefficient of friction $\mu_{m}$ in between the mass and the inclined surface such that the mass does not move is:

& A.3\tan \theta \\\ & B.tan\theta \\\ & C.tan2\theta \\\ & D.2\tan \theta \\\ \end{aligned}$$

Answer 1

We know that friction is the resistive force which tries to oppose the motion of an object. It is a surface phenomenon and is observed only when the object trying to move is in contact with some surface. Which is to say that friction is a contact force.
Formula used:
$\mu_{s}=\dfrac{F_{s}}{F_{n}}$

Complete answer:
Coefficient of static friction is a dimensionless quantity. $\mu_{s}$ is the maximum resistive force applied on any given body such that there is no change in state of the motion. Also, $\mu_{s}$ is the maximum resistive force applied on any given body such that there is no change in state of the motion. It is given as $\mu_{s}=\dfrac{F_{s}}{F_{n}}$, where $F_{s}$ is the applied force and $F_{n}$ is the normal force acting on the given body.
Consider the free body diagram of the rocket at the inclined slope $\theta$. Given that the mass of the rocket $m$ experiences an acceleration of $2\;g$, where $g$ is the gravitational acceleration.

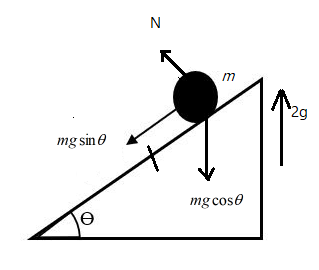
Then the normal force is given as $N=2mgcos\theta+mgcos\theta=3mgcos\theta$, similarly, the frictional force is given as $F=2mgsin\theta+mgsin\theta=3mgsin\theta$
Let the minimum coefficient of friction be $\mu_{m}$. Then the friction force $F$ is given as $F=\mu_{m}N$
$\implies F=3\mu_{m}mgcos\theta$
For the rocket to be in rest, both the frictional forces must be equal to each other, then we have $3\mu_{m}mgcos\theta$=$3mg sin\theta$
$\implies \mu_{m}=tan\theta$

So, the correct answer is “Option B”.

Note:
Friction is a small quantity that acts in the opposite direction to the force. Static friction is the force responsible for an object to be at rest, whereas the kinetic friction is the force that resists the motion of a moving body. Coefficient of static friction is a ratio and has no dimension. It also has no units. Coefficient of static friction depends on the weight of the object and nature of the surface. More the weight, more the static friction and if the surface is rough, then more is the static friction.