Question

A rocket is fired from the earth towards the sun. At what distance from the earth’s centre is the gravitational force on the rocket zero? Mass of the sun $=2\times {{10}^{30}}kg$, mass of the earth $=6\times {{10}^{24}}kg$. Neglect the effect of the other planets etc. (orbital radius $=1.5\times {{10}^{11}}m$).

Answer 1

The force acting on a rocket at a particular distance from the centre of the earth is equal to the sum of forces of attraction of the rocket by the earth as well as the sun. This total force is equated to zero to find the distance of the rocket from the centre of the earth, where the gravitational force is zero.

Formula used:
The force of attraction between two bodies in space is given by
$F=-\dfrac{GMm}{{{R}^{2}}}$
where
$F$ is the force of attraction
$G$ is the gravitational constant
$M$ is the mass of the first body
$m$ is the mass of the second body
$R$ is the distance between the first body and the second body

Complete answer:
Let us consider a rocket fired from the earth to the sun. Let the mass of the rocket be $M$. We are asked to find the distance from the centre of the earth, at which the gravitational force on the rocket is zero. Let this distance be $x$ metres. We are provided that the mass of the sun is equal to $2\times {{10}^{30}}kg$ and the mass of the earth is equal to $6\times {{10}^{24}}kg$. Let us call these masses ${{M}_{s}}$ and ${{M}_{e}}$, respectively. We are also given that the orbital radius of the earth is equal to $1.5\times {{10}^{11}}m$. This orbital radius of the earth is nothing but the distance between the centre of the sun and the centre of the earth. Let us call this distance $r$ meters. The distance between the rocket and the centre of the sun is equal to $(r-x)$ meters as shown in the following figure.

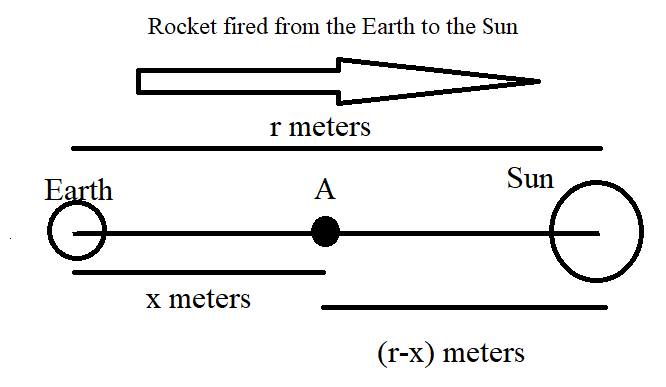
The total force acting on the rocket is equal to the sum of the force of attraction due to the earth and the force of attraction of the sun on the rocket. Let us call this total force ${{F}_{total}}$. Clearly,
${{F}_{total}}={{F}_{e}}+{{F}_{s}}$
where,
we have assumed that the force of attraction on the rocket due to the earth is ${{F}_{e}}$ and the force of attraction on the rocket due to the sun is ${{F}_{s}}$. Let this be equation 1.
Now let us find the values of ${{F}_{e}}$ and ${{F}_{s}}$.
The force of attraction between two bodies in space is given by
$F=-\dfrac{GMm}{{{R}^{2}}}$
where
$F$ is the force of attraction
$G$ is the gravitational constant
$M$is the mass of the first body
$m$ is the mass of the second body
$R$ is the distance between the first body and the second body

Let us use this general equation to find the values of ${{F}_{e}}$ and ${{F}_{s}}$.
Clearly,
${{F}_{e}}=-\dfrac{G{{M}_{e}}M}{{{x}^{2}}}$ is the force of attraction between the earth and the rocket.
${{F}_{s}}=\dfrac{G{{M}_{s}}M}{{{(r-x)}^{2}}}$ is the force of attraction between the sun and the rocket.
Note that the negative sign in the second expression vanishes.

Substituting these values in equation 1, we have
${{F}_{total}}={{F}_{e}}+{{F}_{s}}=-\dfrac{G{{M}_{e}}M}{{{x}^{2}}}+\dfrac{G{{M}_{s}}M}{{{(r-x)}^{2}}}$
Let this be equation 2.

Now, we have to put ${{F}_{total}}=0$in order to find the distance of the rocket from the earth where the gravitational force is zero.
Therefore, let us equate equation 2 to zero as follows.
${{F}_{total}}=-\dfrac{G{{M}_{e}}M}{{{x}^{2}}}+\dfrac{G{{M}_{s}}M}{{{(r-x)}^{2}}}=0$
Clearly,
$\dfrac{G{{M}_{e}}M}{{{x}^{2}}}=\dfrac{G{{M}_{s}}M}{{{(r-x)}^{2}}}\Rightarrow {{\left( \dfrac{\left( r-x \right)}{x} \right)}^{2}}=\dfrac{{{M}_{s}}}{{{M}_{e}}}$
Let this be equation 3.

Substituting the values of ${{M}_{e}},{{M}_{s}}$ and $r$ in equation 3, we have
${{\left( \dfrac{\left( r-x \right)}{x} \right)}^{2}}=\dfrac{{{M}_{s}}}{{{M}_{e}}}=\dfrac{2\times {{10}^{30}}}{6\times {{10}^{24}}}=\dfrac{{{10}^{6}}}{3}\Rightarrow \dfrac{\left( r-x \right)}{x}=\dfrac{{{10}^{3}}}{\sqrt{3}}\Rightarrow 1.732(r-x)={{10}^{3}}x$

Substituting the value of $r$, we have

$1.732(1.5\times {{10}^{11}})=x({{10}^{3}}+1.732)\approx {{10}^{3}}x\Rightarrow x=\dfrac{1.732\times 1.5\times {{10}^{11}}}{{{10}^{3}}}=2.598\times {{10}^{8}}m$

Here, we have taken
${{10}^{3}}+1.732\approx {{10}^{3}}$ because ${{10}^{3}}\gg 1.732$
Therefore, the distance of the rocket from the centre of the earth at which the gravitational force is zero, when the rocket is fired from the earth to the sun is equal to
$x=2.598\times {{10}^{8}}m$

Note:
The force of attraction between two bodies in space follows sign convention. Here, in this question, the force of attraction on the rocket due to the earth is taken as negative because the rocket is moving away from the earth. At the same time, the force of attraction on the rocket due to the sun is taken as positive.