Question
Question: A rocket in a gravity free space burns fuel at a constant rate until time ‘\[{t_0}\]’ when all the f...
A rocket in a gravity free space burns fuel at a constant rate until time ‘t0’ when all the fuel is burnt out. Initially the fuel forms a substantial portion of the mass of the rocket and the velocity of the rocket is zero. Which of the following graphs represents the velocity ‘v’ against time ‘t’ graph for the rocket?
A.
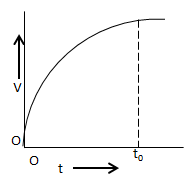
B.
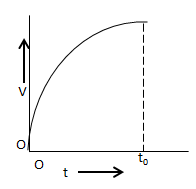
C.
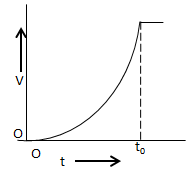
D.
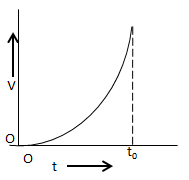
Solution
Use Newton’s first law of motion. This law gives the relation between the velocity of the rocket and the force acting on the rocket.
Complete step by step answer:
When the fuel is burnt, then the velocity of the rock increases.
Initially, as the mass of the fuel is substantial, the velocity of the rocket increases rapidly.
But after time t0, the fuel of the rocket is over. After this time t0, there is no fuel in the rocket to burn and to increase the velocity of the rocket.
Therefore, according to Newton’s first law of motion there is no force on the rocket to increase its velocity as all the fuel is burnt.
Hence, the velocity of the rocket in gravity free space after time t0 remains the same for all time.
In the graph shown in option A, the velocity of the rocket increases rapidly until time t0 and after time t0 also the velocity of the rocket increases slowly.
Hence, the option A is incorrect.
In the graph shown in option B, the velocity of the rocket increases until time t0 and then suddenly becomes zero.
Hence, option B is incorrect.
In the graph shown in option D, the velocity of the rocket increases until time t0 and then suddenly becomes zero.
Hence, the option D is incorrect.
In the graph shown in option C, the velocity of the rocket increases until time t0 and then it becomes constant after time t0.
So, the correct answer is “Option C”.
Note:
According to Newton’s first law of motion, the rocket continues its speed of motion until a force (resulting from burning of fuel) is acting on it and after all the fuel is over, the velocity remains constant.
