Question

A rock is thrown into the air. The height (in feet) of the rock after $t$ seconds is given by $h(t) = - 16{t^2} + 64t$.
A.What is the height reached by the ball after $1$ second?
B.Determine the maximum height the rock attains

Answer 1

For part A we will put the value of $t$ in the given quadric equation and we will get the value of height. for part B we have to solve the general quadratic equation by finding its roots and putting them in the equation.

Complete answer:
A.We have been given a quadratic equation
$h(t) = - 16{t^2} + 64t$
For finding the height in time $t = 1\sec$ , we will get
$\Rightarrow h(1) = - 16 \times {(1)^2} + 64(1)$
$\Rightarrow h(1) = - 16 + 64$
Therefore $h(1) = 48$
So, the height reached by the ball after $1\sec$ is $48ft$.
B.Now for finding the maximum height the rocks attain, first we will find its zeros
$\Rightarrow h(t) = - 16{t^2} + 64t$
$\Rightarrow 16t( - t + 4)$
From here, $t = 0$ and $t = 4$

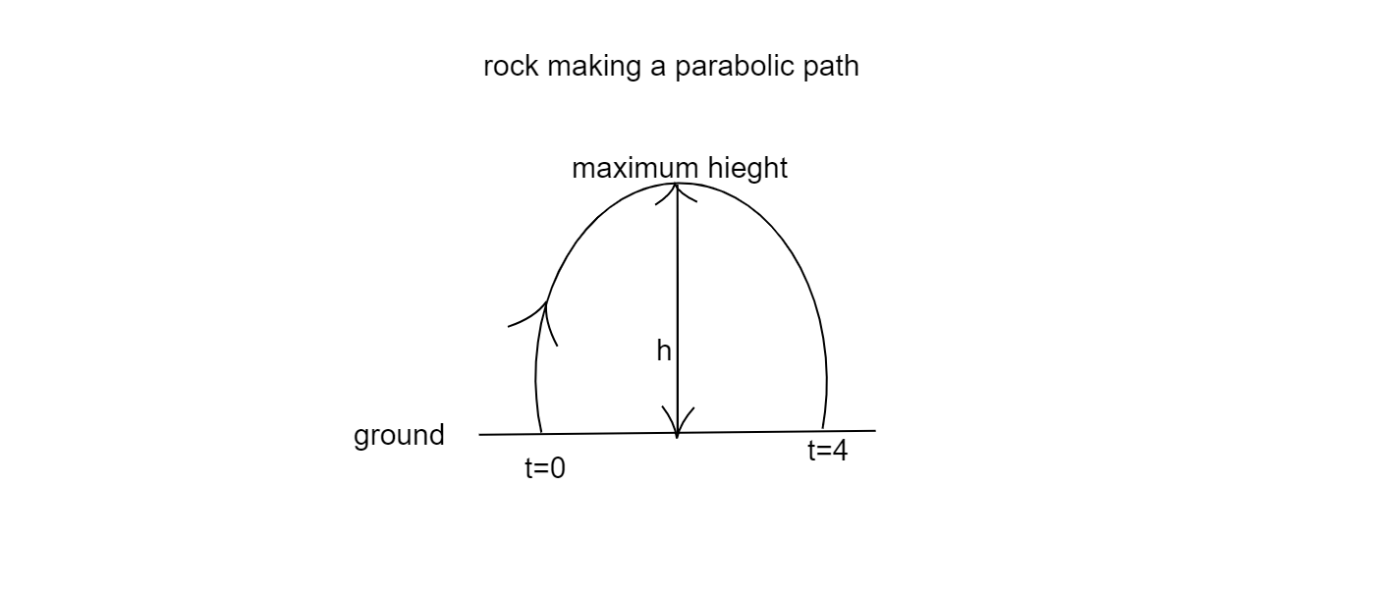
We can see from the given figure the rock makes a parabolic path where at starting the time is $0$and at the end it is $4$ the maximum height is mid way so adding both the zeros and dividing them by $2$ we get the value of $t$
So, $t = \dfrac{{0 + 4}}{2} = 2$
Therefore put $t = 2$ in the given quadratic equation
$\Rightarrow h(2) = - 16 \times {2^2} + 64 \times 2$
Hence $h(2) = 64ft$
The maximum height the rock attains is $64ft$.

Note: Another way of solving this question is to find the vertex of an equation in standard form: $\left( {\dfrac{{ - b}}{{2a}},f\left( {\dfrac{{ - b}}{{2a}}} \right)} \right)$
The general form of the equation is $y = a{x^2} + bx + c$ , x-coordinate is $x = \dfrac{{ - b}}{{2a}}$ by putting the value of $x$we will get y-coordinate, find the value of $a$ and $b$. If the quadratic equation opens down, it will have a maximum value and we will get the maximum height.