Question

A road bridge is in the form of a circular arc of radius $18m$. What is the limiting speed with which a car can traverse the bridge without losing contact at the highest point if the centre of gravity of the car is $0.4m$ above the ground? (in m/s)
(A) 12.36
(B) 13.365
(C) 17.36
(D) 13.428

Answer 1

Hint : When the centrifugal force acting on a body is greater than the forces that hold the object in position then the motion pushes the body to an undesired path of motion. The centrifugal force is fairly a fictitious force, however the situation is a completely practically one. The idea is that the imbalance of forces acting on a body in motion at that instant can cause motion in them.
Formulas used: The formulas that would be used in this problem would be the relation between force acting on a body in motion at that instant. $mg = \dfrac{{m{v^2}}}{r}$ where $m$ is the mass of the body in motion, $g$ is the acceleration due to gravity which is a constant on the surface of the earth, $(g = 9.8m/{s^2})$, $v$ is the velocity of the body in motion, and $r$ is the radius of the rotational axis.

Complete Step by Step answer:
An outward force apparently acting in a rotating reference frame is called the centrifugal force. It is a fictitious inertial force and is only seen when looked at the object from a rotating frame of reference. When viewed from the inertial frame you cannot take this force into account since it would not exist in the inertial frame.
So, consider the case in which a car is moving on a circular arc shaped bridge,

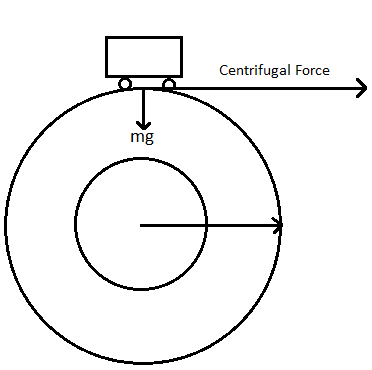
As you can see in the rotational frame of reference the only forces that holds the body in place from being thrown in the gravity while the centrifugal force tries to push it off the bridge. The limitation to stay on the bridge would be, $mg = \dfrac{{m{v^2}}}{r}$ .
We have $r = 18.4m$, so substituting in the equation, (since the centre of gravity of the car is $0.4m$above the ground, $r = {r_b} + {r_g} = 18 + 0.4 = 18.4m$)
$mg = \dfrac{{m{v^2}}}{{18.4}}$ We also know that the acceleration due to gravity, $g = 9.8m/{s^2}$ .
Solving for $v$ to find the limiting velocity to keep the car on the bridge,
${v^2} = \dfrac{{(18.4) \times mg}}{m}$ cancelling out the common terms, ${v^2} = 18.4 \times g$
$\Rightarrow v = \sqrt {18.4 \times 9.8} = \sqrt {180.92}$
$\Rightarrow v = 13.45m/s$
Thus, the limiting velocity of the vehicle should be $v = 13.45m/s$.

Hence the correct answer is option D.

Note: We have used a linear velocity variable to define the rotational parameter centrifugal force, because${F_c} = m{\omega ^2}r$. But we know that $\omega = \dfrac{v}{r}$ . Thus, substituting the value, we get, ${F_c} = \dfrac{{m{v^2}}}{r}$.