Question

A river is flowing with a speed of 1 Km/hr. A swimmer wants to go to point C starting from A. He swims with a speed of 5 Km/hr. at angle $\theta$ w.r.t the river flow. If AB = BC = 400m. Then find the value of $\theta$ in degrees.

Answer 1

In this particular type of question first draw the pictorial representation and marks all the point it will give us a clear picture of what we have to calculate then rotate the component of velocity of the swimmer in horizontal and in vertical direction and equate them in order to reach the point C so use these concepts to reach the solution of the question.

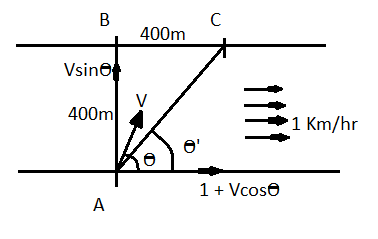
The angle the swimmer makes with the horizontal is $\theta$ w.r.t the river flow as shown in the above figure.
Let the velocity of the swimmer is V Km/h. as shown in the figure.
Now rotate the component of velocity in horizontal direction and in the vertical direction.
So the horizontal component of velocity of the swimmer is, ${V_x} = V\cos \theta$
And the vertical component of velocity of the swimmer is, ${V_y} = V\sin \theta$
Now it is given that the velocity of the river which is flowing in the horizontal direction is 1Km/hr.
And the velocity of a swimmer is 5Km/hr.
So, V = 5Km/hr.
The total velocity in the horizontal direction = velocity of river + component of velocity of swimmer in horizontal direction.
So the total velocity in the horizontal direction = $\left( {1 + 5\cos \theta } \right)$ Km/hr.
And total velocity in the vertical direction = $5\sin \theta$ Km/hr.
Now if we join the points A and C so the line AC makes an angle $\theta '$ with the horizontal as shown in the figure which is given as,
$\Rightarrow \theta ' = {\tan ^{ - 1}}\left( {\dfrac{{AB}}{{BC}}} \right)$
Now it is given that, AB = BC = 400
$\Rightarrow \theta ' = {\tan ^{ - 1}}\left( {\dfrac{{400}}{{400}}} \right) = {\tan ^{ - 1}}\left( 1 \right) = {45^o}$
So in order to get to point C, the horizontal component of velocity of the swimmer is equal to the vertical component of velocity of the swimmer.
$\Rightarrow \left( {1 + 5\cos \theta } \right) = 5\sin \theta$
Now squaring on both sides we have,
$\Rightarrow {\left( {1 + 5\cos \theta } \right)^2} = {\left( {5\sin \theta } \right)^2}$
Now expand the square we have,
$\Rightarrow 1 + 25{\cos ^2}\theta + 10\cos \theta = 25{\sin ^2}\theta$
$\Rightarrow 1 + 25{\cos ^2}\theta + 10\cos \theta = 25\left( {1 - {{\cos }^2}\theta } \right)$, $\left[ {\because {{\sin }^2}\theta = 1 - {{\cos }^2}\theta } \right]$
$\Rightarrow 1 + 25{\cos ^2}\theta + 10\cos \theta = 25 - 25{\cos ^2}\theta$
$\Rightarrow 50{\cos ^2}\theta + 10\cos \theta - 24 = 0$
Now divide by 2 throughout we have,
$\Rightarrow 25{\cos ^2}\theta + 5\cos \theta - 12 = 0$
Now this is a quadratic equation so apply quadratic formula we have,
$\Rightarrow \cos \theta = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}$, where, b = 5, a = 25 and c = -12
$\Rightarrow \cos \theta = \dfrac{{ - 5 \pm \sqrt {{5^2} - 4\left( {25} \right)\left( { - 12} \right)} }}{{2\left( {25} \right)}}$
$\Rightarrow \cos \theta = \dfrac{{ - 5 \pm \sqrt {25 + 1200} }}{{50}}$
$\Rightarrow \cos \theta = \dfrac{{ - 5 \pm \sqrt {1225} }}{{50}}$
$\Rightarrow \cos \theta = \dfrac{{ - 5 \pm 35}}{{50}},\left[ {\because \sqrt {1225} = 35} \right]$
$\Rightarrow \cos \theta = \dfrac{{ - 5 + 35}}{{50}},\dfrac{{ - 5 - 35}}{{50}}$
$\Rightarrow \cos \theta = \dfrac{{30}}{{50}},\dfrac{{ - 40}}{{50}}$
$\Rightarrow \cos \theta = \dfrac{3}{5},\dfrac{{ - 4}}{5}$
As $\theta$ lie in the first quadrant, and cos$\theta$ is positive in the first quadrant so negative value is not possible.
$\Rightarrow \cos \theta = \dfrac{3}{5}$
$\Rightarrow \theta = {\cos ^{ - 1}}\dfrac{3}{5} = {53^o}$
So this is the required angle the swimmer makes with the horizontal so that he reaches the point C.
Note: Whenever we face such types of questions the key concept we have to remember is that if the velocity makes an angle x with the horizontal then its horizontal component is cos x and its vertical component is cos (90 – x) = sin x, and always recall the formula to solve the complex quadratic equation which is stated above.