Question

A river is flowing from West to East at a speed of $5m$ per min. If a swimmer standing on the South Bank of the river wants to swim across the river in the shortest time, then he should swim in a direction (speed of swimmer in still water)
(A) ${30^o}$ East-North
(B) Due North
(C) ${30^o}$ West-North
(D) ${60^o}$ East-North

Answer 1

Let us consider a river and the velocity of the flow of the river is known. A swimmer must cross the river from one point to another. As the river is flowing the swimmer should jump to the river in the reverse direction of the flow of the river. We can also find the angle of the direction by representing it in the figure.

Complete Step By Step Answer:
The speed of the flow of the river is given as ${v_r} = 5m{\min ^{ - 1}}$ .
There is a swimmer who must cross the river from one point on the south bank to another point on the north bank. It is said that the swimmer can swim in still water with a speed of ${v_s}$ .
For the swimmer to reach the north bank, he must jump from the initial point making an angle $\theta \;$ with the vertical. When the swimmer jumps by making an angle $\theta \;$ , the direction should be opposing the direction of the flow of the river. I.e. the direction of the will be west north. When he jumps in the west north direction by making the angle $\theta \;$ , the swimmer will have his speed ${v_s}$ and the river will have a speed of ${v_r} = 5m{\min ^{ - 1}}$ .

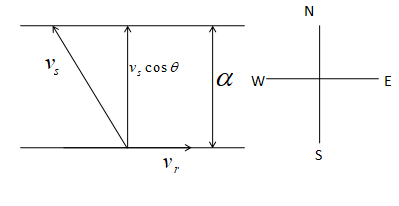
Consider the figure.
The given conditions can be represented as in the figure. Let us consider the distance to be $\alpha$
Time is taken to cross the river, $t = \dfrac{\alpha }{{{V_S}cos\theta }}$
for time to be minimum, $cos\theta = \;maximum$
$\Rightarrow \theta = {0^o}$
so, summer should swim due North.
Hence Option B is correct.

Note:
If the swimmer jumps straight from one point A to the river, he will not reach another point B. Since the swimmer has a certain speed in the north direction and the river has a speed of ${v_r} = 5m{\min ^{ - 1}}$ from west to the east direction. Therefore the direction of the swimmer is the resultant of the two velocities.