Question
Question: A ring which can slide along the rod is kept at the midpoint of a smooth rod of length L. The rod is...
A ring which can slide along the rod is kept at the midpoint of a smooth rod of length L. The rod is rotated with a constant angular velocity ω about the vertical axis passing through one of its ends. Ring is released from mid point. Find the velocity of the ring when it just leaves the rod.
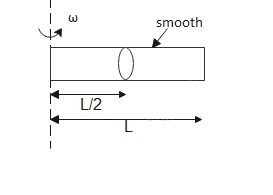
Solution
Usually, a centrifugal force acts when subjected to angular velocity. So, first we have to apply the formula of centrifugal force. Then, acceleration is expressed as a rate of change of velocity and integrated. Finally, the formula for velocity is applied and from this the actual velocity of the ring at the time at which it leaves the rod is evaluated.
Complete answer:
The given data are
Length = L
Angular velocity = ω
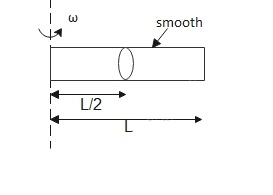
We need to calculate the velocity of the ring
Using centrifugal force
mω2x = ma ---(1)
Let this be equation (1)
Where,
m is the mass
ω is the angular velocity
a is the acceleration
x is the distance
Substitute a=dxvdvin equation (1)
Where, v is the velocity
We get,
ω2x =dxvdv
ω2xdx =vdv ----(2)
Let this be equation (2)
Integrating equation (2) on both sides, we get
2L∫Lω2xdx=0∫vvdv
ω2(2x2)2LL=(2v2)0v
ω2(2L2−8L2)=(2v2) ----(3)
Let this be equation (3)
Taking square root on both sides of equation (3),
We get,
v=23ωL -----(4)
We need to the calculate the velocity at time of leaving rod
Using formula for velocity
(v1)2= (ωL)2+ (23ωL)2
(v1)= (ωL)2+ (23ωL)2
(v1)= 27ωL
Hence, The velocity of the ring at the time of leaving rod is
27ωL
Answer is 27ωL
Note:
There may be another case where the whole length of the rod is taken into account. In such cases, where we might have to find velocity for the whole length of the rod by certain tricks. That is, we have to substitute x = l and find the value of the velocity directly.
