Question

A ring shaped tube contains two ideal gases with equal masses and molar masses ${{M}_{1}}$ =32 and ${{M}_{2}}$=28. The gases are separated by one fixed partition P and another movable stopper S which can move freely without friction inside the ring. The angle α in degree is

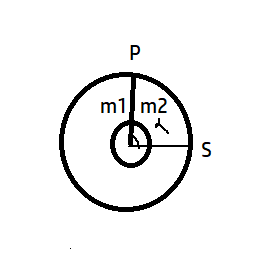
(A) 182
(B) 170
(C) 192
(D) 180

Answer 1

In this problem it is mentioned that masses of the gas in the ring are the same. Also, they are separated by fixed portions. Thus, the pressure exerted must be the same by both the gases.

Complete step by step answer:
Pressure exerted by gas A= pressure exerted by gas B
Using ideal gas law, PV=nRT
$P=\dfrac{nRT}{V}$
So ${{P}_{1}}={{P}_{2}}$
$\dfrac{{{n}_{1}}RT}{{{V}_{1}}}=\dfrac{{{n}_{2}}RT}{{{V}_{2}}}$here temperature of the both of them are same and R is a gas constant.
Let us find out the number of moles, it is given by the formula. $n=\dfrac{m}{M}$
Here m is the given mass and M is the molecular mass of the gas. It is given that the given mass for both of the gas are the same.
$\dfrac{{{n}_{1}}}{{{V}_{1}}}=\dfrac{{{n}_{2}}}{{{V}_{2}}}$
$\Rightarrow \dfrac{32}{{{V}_{1}}}=\dfrac{28}{{{V}_{2}}}$
$\Rightarrow \dfrac{{{V}_{2}}}{{{V}_{1}}}=\dfrac{8}{7}$------(1)
It is clear from the figure that total angle is ${{360}^{0}}$ and gas 2 makes an angle $\alpha$. Since radius for both is same, thus,
$\dfrac{{{V}_{2}}}{{{V}_{1}}}=\dfrac{\alpha }{360-\alpha }$
Comparing it with eq (1) we get,

& \dfrac{8}{7}=\dfrac{\alpha }{360-\alpha } \\\ & \Rightarrow 7\alpha =8\times 360-8\alpha \\\ & \Rightarrow 15\alpha =2880 \\\ & \Rightarrow \alpha =192 \\\ \end{aligned}$$ Thus, the angle came out to be 192 degrees. Hence, the correct option is (C). **Note:** We have used ideal gas law here because it was mentioned in the question that the gas is ideal. Otherwise we would have to use real gas laws. Also while finding volume we have taken the ratio of angles as the radii for both are the same.