Question

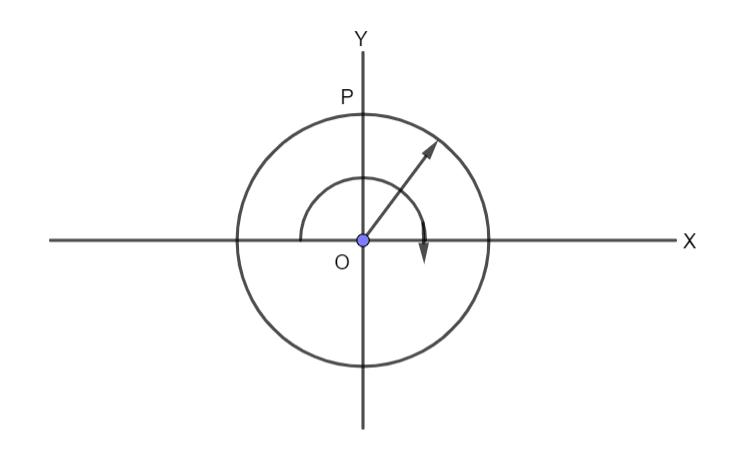
A ring rotates about the z axis as shown in the figure. The plane of rotation is x-y. At a certain instant, the acceleration of a particle P (shown in the figure) is $(6\hat i - 8\hat j)\,m\,{s^{ - 2}}$ . Find the angular acceleration of the ring and the angular velocity at that instant. Radius of the ring is $2\,m$ .

Answer 1

In this question, we will break the given acceleration into its components- tangential and normal- and use their formulas. The tangential acceleration will be equal to the x component of the given acceleration and the normal acceleration is equal to the y component of the given acceleration. Given that the radius of the circular path is 2m, we can find out the value of angular velocity and angular acceleration by substituting the values.

Complete step by step answer:
Let the angular acceleration be $\alpha$ and the angular velocity be $\omega$ .
The acceleration of a particle moving in circular motion has two components.
(1) Tangential acceleration: The acceleration that acts along the tangent. This is generally denoted as ${a_t}$ . The magnitude is given by ${a_t} = R\alpha$ where R is the radius of the circular path.
(2) Normal or centripetal acceleration: The acceleration acting radially inwards towards the center of the circular path described by the body. This is generally denoted as ${a_n}$ . The magnitude is given by ${a_n} = R{\omega ^2}$ where R is the radius of the circular path.
At point P, the tangential acceleration will be equal to the x component of the given acceleration and the normal acceleration is equal to the y component of the given acceleration.
Hence, we can say that ${a_t} = R\alpha = 6\,rad\,{s^{ - 2}}$
Given that the radius of the circular path is 2m, we can find out the value of angular acceleration.
Substituting the values, we get,
$6 = 2\alpha$
$\Rightarrow \alpha = 3\,rad\,{s^{ - 2}}$
Also, we can say that ${a_n} = R{\omega ^2} = 8\,rad\,{s^{ - 2}}$
Given that the radius of the circular path is 2m, we can find out the value of angular velocity.
Substituting the values, we get,
$8 = 2{\omega ^2}$
$\Rightarrow {\omega ^2} = 4$
This gives us $\omega = 2\,rad\,{s^{ - 1}}$

Note: Here we did not take into account the vectorial notation of accelerations. Acceleration being a vector must be given some direction. However, in this question, the components were already given and hence the direction of the acceleration was also already specified. So, we directly calculated the magnitude of the angular acceleration and angular velocity from the formulas.