Question

A ring rolls without slipping on a horizontal surface. At any instant, its position is as shown in the figure.

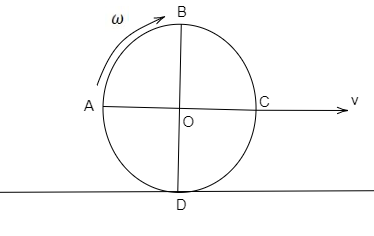
A) Section ABC has greater kinetic energy than section ADC.
B) Section BC has greater kinetic energy than section CD.
C) Section BC has the same kinetic energy as section DA.
D) The section AB, BC, CD, and DA have the same kinetic energy.

Answer 1

The ring is rolling without slipping which means that there is no relative motion between the ring and the ground. The instantaneous velocity between point D and ground is zero but the instantaneous velocity of other points is not zero with respect to ground.

Complete step by step answer:
The instantaneous centre of rotation is point D, the velocity of any point is equal to $v = \omega \times r$ where v is the velocity, $\omega$ is angular velocity and $r$ is the distance from the point D to the other point.
The velocity of point A is given by,
$v = \omega \times r$
As the angular velocity of the body is same for all the points but the radius is different and for point A,
$r = \sqrt 2 r$
So the velocity will be,
$\Rightarrow {v_A} = \omega \times \sqrt 2 r$
As the distance of the point, C is also the same and equal to point A.
Therefore, the velocity of the point C is given by,
$\Rightarrow {v_C} = \omega \times \sqrt 2 r$.
Now let us calculate the value of the velocity of point B.
As the velocity is given by $v = \omega \times r$ also the distance from point D to point B is equal to $2r$.
So the velocity of the point is given by${v_B} = \omega \times r$.
$\Rightarrow {v_B} = \omega \times r$
$\Rightarrow {v_B} = \omega \times 2r$
As the kinetic energy depends upon the velocity of the points or the body. Therefore it can be observed that the kinetic energy of the section ABC is more than the kinetic energy of section ADC. Also, section BC will have greater kinetic energy than the section CD.

Therefore, the correct options are option A and option B.

Note:
The centre of rotation of the body is a point where there is no relative motion between the body and ground and in this case, it is point D. The velocity of the different points are calculated by taking the distance from the centre of rotation.