Question

A ring of radius $R$ is with uniformly distributed charge $Q$ on it. A charge $q$ is now placed at the centre of the ring. Find the increment in tension in the ring.

Answer 1

In this question, calculate the linear charge density of the ring and represent the linear charge density by $\lambda$. Linear charge density is directly proportional to the charge stored and inversely proportional to the circumference of the ring.

Complete step by step answer As we know that when a charge $+ q$ is placed at the centre of the ring, the wire gets stretched due to mutual electrostatic repulsion between the positive charge and each element of the wire having positive charge $dQ$. And stretching causes the internal restoring forces resulting in an additional tension in the wire of the ring.
Now we consider the figure $\left( 1 \right)$ as,

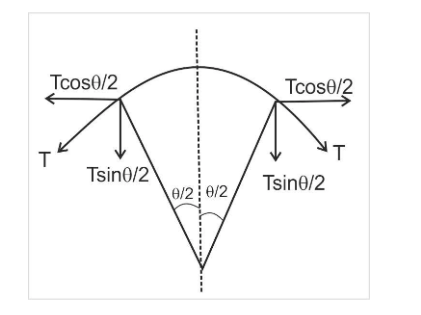
Figure$\left( 1 \right)$

Let us consider the linear charge density of the ring is $\lambda$. The linear density is the charge per unit length. Linear density tells about the charge stored in a particular area.
$\Rightarrow \lambda = \dfrac{Q}{{2\pi R}}$
Where, $Q$ is the charge $R$ is the radius of the ring.
Now, calculate the force acting between a small section $dx$ of the ring and the charge $q$ in the centre will be,
$\Rightarrow T = \dfrac{{kq\lambda dx}}{{{R^2}}}......\left( 1 \right)$
Where, $T$ is the force acting in a small section of the ring.
Now consider, if $\theta$ be the angle subtended at the center by $dx$. $\theta$ is very small, and the force acting in the small section of the ring will be,
$\Rightarrow T\theta = 2T\sin \dfrac{\theta }{2}$
We can write
$\Rightarrow \dfrac{{dx}}{R} = \theta$
Now, we substitute the value in equation (1) as,
$\Rightarrow T = \dfrac{{kq\lambda \theta }}{R}$
Therefore, the force should be equal to $T = \dfrac{{kq\lambda \theta }}{R}$.
Now, substitute the value of $\lambda$ in the force equation as,
$\Rightarrow T = \dfrac{{kq\left( {\dfrac{Q}{{2\pi R}}} \right)\theta }}{R}$
We know that the value of $k$ is $\dfrac{1}{{4\pi {\varepsilon _0}}}$, so the equation become
$\therefore T = \dfrac{{Qq}}{{8{\pi ^2}{\varepsilon _0}{R^2}}}$

Therefore, the increment in the tension of the ring will be equal to $\dfrac{{Qq}}{{8{\pi ^2}{\varepsilon _0}{R^2}}}$.

Note: As we know that, if the angle $\theta$ be the angle subtended at the centre by $dx$. The angle $\theta$ is very small, and the force acting in the small section of the ring will be equal to the charge stored in the particular area.