Question

A ring of radius $r = 25cm$ made of lead wire is rotated about a stationary vertical axis passing through its center and perpendicular to the plane of the ring. The angular speed in $rps$ at which the ring ruptures is $(20 + x)$. The value of $x$ is:

Answer 1

- Hint: You can start by assuming a small section on the ring $\theta$ . Then draw a well-labelled diagram including all the forces acting on the ring. Then compare the inwards and outwards forces on the ring that will give you this equation ${F_C} = 2T\sin \dfrac{\theta }{2}$. Then use the equation $F = ma$ and compare the two equations of force to get this equation $m{\omega ^2}R = T\theta$. Then use the equation $\because \rho = \dfrac{m}{V}$ and obtain the value of $m$ and substitute this value into $m{\omega ^2}R = T\theta$ to reach the solution.

Complete step-by-step answer:
In the given situation the ring will only break if the tension on the ring will be equal to the breaking stress of the wire.
Let’s consider a small section of the ring $\theta$ (Assuming $\theta$ is very small)

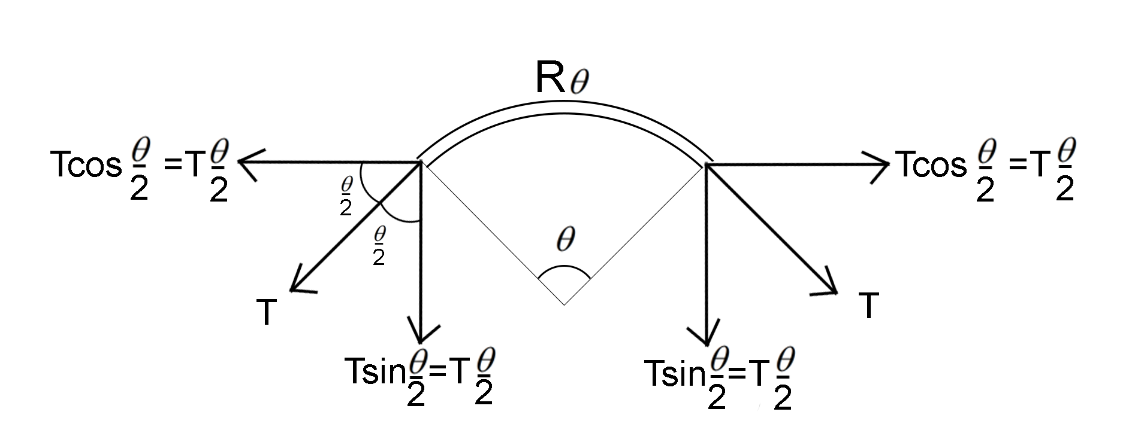
Now, we know
In vertical direction the ring experiences an upwards force equal to the downwards force that the two ends experience
${F_C} = 2T\sin \dfrac{\theta }{2}$
${F_C} = T\theta$( $\because \theta$ is small)(Equation 1)
We know that acceleration of a rotating body is
$a = {\omega ^2}R$
And force is given by
$F = ma$
$F = m{\omega ^2}R$ (Equation 2)
Comparing equation 1 and 2, we get
$m{\omega ^2}R = T\theta$
$\because \rho = \dfrac{m}{V}$
$\therefore \rho V{\omega ^2}R = T\theta$ (Equation 3)
We know that
$V = l \times A$
Here $V =$ Volume
$l =$ Length
$A =$ Area of cross-section
$V = R\theta (2\pi {R^2})$
Using this value of $V$in equation 3, we get
$\rho \theta \pi {R^4}{\omega ^2} = T\theta$
$\Rightarrow T = \rho \pi {R^4}{\omega ^2}$
We know that stress is
$Stress = \dfrac{{Force}}{{Area}}$
Let $\sigma$ be the breaking stress of the lead wire, so
$F = \sigma \pi {R^2}$
We know that for the ring to rupture
$\rho \pi {R^4}{\omega ^2} \geqslant \sigma \pi {R^2}$
So at the minimum for the ring to break
$\rho \pi {R^4}{\omega ^2} = \sigma \pi {R^2}$
$\omega = \sqrt {\dfrac{\sigma }{{\rho {R^2}}}}$
We know that the frequency ( $f$ or also called $rps$ ) is given by
$f = \dfrac{\omega }{{2\pi }}$
$f = \dfrac{1}{{2\pi R}}\sqrt {\dfrac{\sigma }{\rho }}$
We know that
$\sigma = 1.5 \times {10^7}N{m^{ - 2}}$
And $\rho = 11.3$
$\therefore f = 23rps$
Given, $f = 20 + x$
$23 = 20 + x$
$x = 3$
Hence, the value of $x$ is $3$ .

Note: The concept of stress used in this question is a very important concept. From a bridge to your smartphone every object is quality controlled based on a number of standards. This quality testing is very important because we don’t want our possessions to break during daily use and last us a long time.