Question
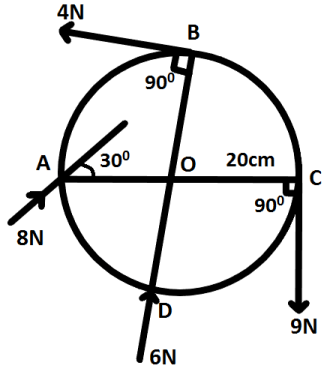
Question: A ring of radius \( 20cm \) and mass \( 100g \) is acted upon by our forces as shown in figure. The ...
A ring of radius 20cm and mass 100g is acted upon by our forces as shown in figure. The angular velocity required by it in 2s starting from the rest is:
(A) 90rad/s
(B) 900rad/s
(C) 180rad/s
(D) 950rad/s
Solution
Hint : To solve this question, we will first find the total torque applied on the ring. Then by using the relationship between torque and angular acceleration, we will find the angular acceleration of the ring. And finally, using this acceleration and time given, we will find the angular velocity of the ring.
τ=Frsinθ , where, τ is the torque, F is the force, r is the radius of the ring, θ is the angle through which the force is applied
τ=Iα , where, τ is the torque, I is the moment of inertia of the ring about its centre and α is the angular acceleration.
I=mr2 , where, I is the moment of inertia of the ring about its centre, m is the mass of the ring and r is the radius of the ring
ω=αt , where, α is the angular acceleration, ω is the angular velocity and t is the time.
Complete Step By Step Answer:
First we will find the total torque for which we need to find the torque due to individual forces applied on the body. We will take compressive force as negative and tensile force as positive.
τA=FArsinθA=−8×0.2×sin30=−8×0.2×21=−0.8Nm
τB=FBrsinθB=4×0.2×sin90=4×0.2×1=0.8Nm
τC=FCrsinθC=9×0.2×sin90=9×0.2×1=1.8Nm
Now, the line of force applied at point D passes through the centre of the ring. Therefore,
τD=FD×0=−6×0=0Nm
Thus, we can say that the total torque is given by:
τ=τA+τB+τC+τD=−0.8+0.8+1.8−0=1.8Nm
Now, we will find the angular acceleration.
We know that τ=Iα and I=mr2
⇒τ=mr2α ⇒α=mr2τ
We have τ=1.8Nm , m=100g=0.1kg and r=20cm=0.2m .
⇒α=0.1×0.221.8=450rad/s2
We know that angular velocity can be given by the formula ω=αt and we are asked to find the angular velocity for the time period of 2s .
⇒ω=αt=450×2=900rad/s
Hence, option B is the right answer.
Note :
Here, we have used the formula for the moment of inertia of the ring about its centre which is I=mr2 . However, if the solid disc is given instead of the ring this formula becomes I=21mr2 . The procedure for the disc remains the same except this change in its moment of inertia.
