Question

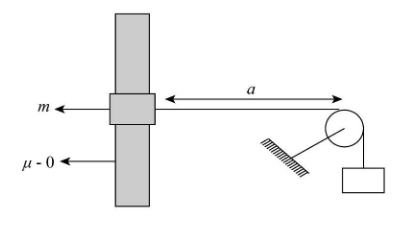
A ring of mass m slides on a smooth vertical rod. A light string is attached to the ring and is passing over a smooth peg distant from the rod, and at the other end of the string is a mass $M\left( {M > m} \right)$. The ring is held on a level with the peg and released. Show that it first comes to rest after falling a distance $\dfrac{{2mMa}}{{{M^2} - {m^2}}}$.

Answer 1

The above problem is resolved using the kinematics concepts and fundamentals as well as the basic formulation regarding the heights and distances. Moreover, the condition for the equilibrium is applied to solve the problem like this. The potential energy for both the entities are conserved, as per the given analysis.

Complete step by step answer:
Refer the given diagram to conclude that the system starts from rest. Let us consider that after it is released the system achieves the rest condition again (instantaneously) when the ring falls at a distance y, below the initial position and the block is raised by the distance h.
There will be some loss in the potential energy and this is gained by the block, since neither mass has kinetic energy at that instant. Then the potential energies are,
$mgy = Mgh$
Here, g is the gravitational acceleration.
The length (L) of the string between the peg and the ring is L where,
${L^2} = {a^2} + {y^2}$
The value of L is $L = \left( {a + h} \right)$.
On substituting the values in the above equation, we get,

{L^2} = {a^2} + {y^2}\\\ {\left( {h + a} \right)^2} = {a^2} + {y^2}\\\ {a^2} + {h^2} + 2ah = {a^2} + {y^2}\\\ {y^2} = {h^2} + 2ah \end{array}$$ Let the value of spring constant k is $$k = \dfrac{m}{M}$$ and the value of h is $$h = ky$$. Again, on applying the values in the above equation, $$\begin{array}{l} {h^2} = {y^2} - 2ah\\\ {\left( {ky} \right)^2} = {y^2} - 2a\left( {ky} \right)\\\ \left( {1 - {k^2}} \right)y = 2ak\\\ y = \dfrac{{2ak}}{{\left( {1 - {k^2}} \right)}} \end{array}$$ On further solve the above equation as, $$\begin{array}{l} y = \dfrac{{2ak}}{{\left( {1 - {k^2}} \right)}}\\\ y = \dfrac{{2a\left( {\dfrac{m}{M}} \right)}}{{\left( {1 - {{\left( {\dfrac{m}{M}} \right)}^2}} \right)}}\\\ y = \dfrac{{2amM}}{{\left( {{M^2} - {m^2}} \right)}} \end{array}$$ Therefore, the falling distance is $$\dfrac{{2amM}}{{\left( {{M^2} - {m^2}} \right)}}$$. **Note:** To resolve the given problem, one must have a clear view of concepts like the conservation of energy and the condition of equilibrium. Here in this problem, the equilibrium condition is applied to balance the forces being applied. The conservation of energy has significant importance, as the energy is conserved in the given case.