Question

A ring of mass $M$ and radius $R$ is placed directly above a uniform sphere of mass $8M$ and same radius $R$. The centre of the ring is at a distance $d = \sqrt 3 R$ from the centre of the sphere. Find the gravitational attraction between the ring and the sphere.
A) $\dfrac{{8G{M^2}}}{{{R^2}}}$
B) $\dfrac{{2G{M^2}}}{{\sqrt 3 {R^2}}}$
C) $\dfrac{{3G{M^2}}}{{2{R^2}}}$
D) $\dfrac{{\sqrt 3 G{M^2}}}{{{R^2}}}$

Answer 1

Here we have to first consider a point on the axis of the ring at distance $d$ from its centre and obtain the gravitational field experienced at this point on the axis. Then we can obtain the gravitational force experienced by the sphere which is at the same distance as the product of the gravitational field at that point and the mass of the sphere.

Formulas used:
-The gravitational field experienced by a point on the axis of a ring is given by, ${E_x} = \dfrac{{GMx}}{{{{\left( {{r^2} + {x^2}} \right)}^{3/2}}}}$ where $G$ is the gravitational constant, $M$ is the mass of the ring, $x$ is the distance between the point and the centre of the ring and $r$ is the radius of the ring.
-The gravitational force experienced by a body is given by, $F = {E_x}m$ where ${E_x}$ is the gravitational field experienced by the body at a distance $x$ and $m$ is the mass of the body.

Complete step by step answer.
Step 1: Sketch a figure depicting the arrangement of the ring and the sphere.

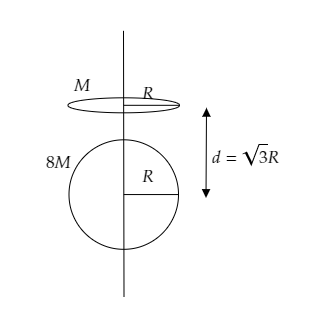
In the above figure, we have a ring placed directly above a sphere at some distance.
The mass of the ring is ${m_r} = M$ and that of the sphere is ${m_s} = 8M$ . The radius of both the ring and the sphere is the same and it is given to be $R$ .
Also, the distance between the centre of the sphere and that of the ring is given to be $d = \sqrt 3 R$ .
Step 2: Express the gravitational field experienced at a point along the axis of the ring at a distance $d = \sqrt 3 R$ from the centre of the ring.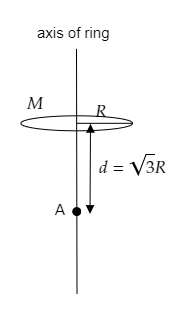

The gravitational field experienced by a point on the axis of a ring can be expressed as ${E_x} = \dfrac{{GMx}}{{{{\left( {{r^2} + {x^2}} \right)}^{3/2}}}}$ ----------- (1)
where $G$ is the gravitational constant, $M$ is the mass of the ring, $x$ is the distance between the point and the centre of the ring and $r$ is the radius of the ring.
In our case, $x = d = \sqrt 3 R$ and $r = R$ .
So the gravitational field experienced at point A will be ${E_d} = \dfrac{{GM\sqrt 3 R}}{{{{\left( {{R^2} + {{\left( {\sqrt 3 R} \right)}^2}} \right)}^{3/2}}}}$
On simplifying the above expression becomes ${E_d} = \dfrac{{GM\sqrt 3 R}}{{{{\left( {4{R^2}} \right)}^{3/2}}}} = \dfrac{{\sqrt 3 GM}}{{8{R^2}}}$
Thus the gravitational field experienced at A is ${E_d} = \dfrac{{\sqrt 3 GM}}{{8{R^2}}}$ .
Step 3: Express the gravitational force experienced by the sphere at the same distance.
The gravitational force experienced by the sphere can be expressed as $F = {E_d}{m_s}$ -------- (2)
Substituting for ${E_d} = \dfrac{{\sqrt 3 GM}}{{8{R^2}}}$ and ${m_s} = 8M$ in equation (2) we get, $F = \dfrac{{\sqrt 3 GM}}{{8{R^2}}} \times 8M = \dfrac{{\sqrt 3 G{M^2}}}{{{R^2}}}$
Thus the gravitational force between the sphere and the ring is $F = \dfrac{{\sqrt 3 G{M^2}}}{{{R^2}}}$ .

So the correct option is D.

Note: In the arrangement mentioned in the question we observe from our sketched figure that the centre of the ring and the centre of the sphere lie along the axis of the ring. So we consider point A at distance $d = \sqrt 3 R$ on the axis of the ring while obtaining the gravitational field experience at that point. This point will thus correspond to the centre of the sphere.