Question
Question: A ring of mass \[m\] and radius \[R\] has three particles attached to the ring as shown in the figur...
A ring of mass m and radius R has three particles attached to the ring as shown in the figure. The centre of the ring has a speed v0. If the kinetic energy of the system is xmv02. Find x (Slipping is absent)
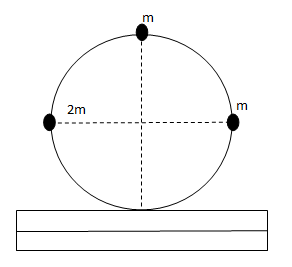
Solution
The kinetic energy of the system is given and we are asked to find the value of x. To find the value of x we have to calculate the kinetic energy of the system. For this, first find the kinetic energy of each particle and then kinetic energy of the ring and equate the kinetic energy of the system obtained with the given value.
Complete step by step answer:
Given, velocity of centre is v0
As the velocity of the centre is v0, so each point on the ring will move with the same velocity that is v0. So, all three particles attached to the ring will also move with the same velocity v0. Let us assume the ring is moving towards right or rotating in clockwise direction.
Let us draw a diagram,
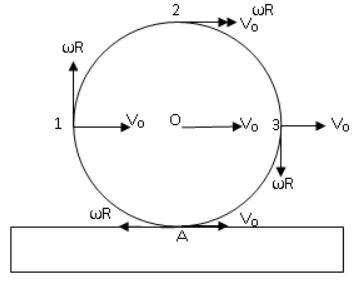
Let O be the centre and A be the point of contact between ring and block, ω be the angular velocity of the ring and R be the radius of the ring. It is given that the slipping is absent, if slipping is absent then at the point of contact the velocity will be zero. That is at point A velocity is zero and this is possible only when
ωR=v0 (i)
Now, let us find the kinetic energy of each particle.
For particle 1, let v1 be its velocity. We observe that v1 is the resultant velocity of v0 and ωRand angle between them is 90∘. So, v1 can be written as,
v1=v02+(ωR)2+2v0ωRcos90∘
We have, ωR=v0 , that is
