Question

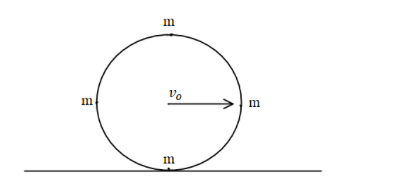
A ring of mass m and radius R has four particles each of mass m attached to the ring as shown in the figure. The centre of the ring has a speed${v_o}$. The kinetic energy of the system is:

A) $m{v^2}_o$.
B) $3m{v^2}_o$.
C) $5m{v^2}_o$.

D) $6m{v^2}_o$

Answer 1

Kinetic energy is defined as the energy of the system obtained due to virtue of its motion. Linear velocity of the particle is equal to the product of angular velocity and radius of the circle and the direction of the velocity of the particle is always to the perpendicular to the line joining the point at which velocity is being is calculated and the point of contact with ground.

Formula used: The formula of the linear velocity is given by,
$\Rightarrow v = \omega \times R$
Where the linear velocity is v the angular velocity is $\omega$ and the radius is R.
The formula of the kinetic energy is equal to,
$\Rightarrow K \cdot E = \dfrac{1}{2}m{v^2}$
Where K.E is kinetic energy the mass of the object is m the velocity of the object is v.

Complete step by step solution:
It is given in the problem that a ring of mass m and radius R has four particles each of mass m attached to the ring. The centre of the ring has a speed${v_o}$. We need to find the kinetic energy of the system.
The linear velocity of the centre of the ring is given as${v_o}$.
The relation for the centre of the circle is equal to,
$\Rightarrow {v_o} = \omega \times R$
Therefore the angular velocity is equal to,
$\Rightarrow \omega = \dfrac{{{v_o}}}{R}$………eq. (1)

The linear velocity of the particle at point A is,
$\Rightarrow v = \omega \times R$
$\Rightarrow {v_A} = \omega \times 2R$
Replacing the value of equation (1) in above relation.
$\Rightarrow {v_A} = \omega \times 2R$
$\Rightarrow {v_A} = \left( {\dfrac{{{v_o}}}{R}} \right) \times 2R$
$\Rightarrow {v_A} = 2{v_o}$………eq. (2)
The kinetic energy at point A is equal to,
$\Rightarrow K \cdot E = \dfrac{1}{2}m{v_A}^2$
Replacing the value of the velocity from the equation (2).
$\Rightarrow K \cdot {E_A} = \dfrac{1}{2}m{v_A}^2$
$\Rightarrow K \cdot {E_A} = \dfrac{1}{2}m{\left( {2{v_o}} \right)^2}$
$\Rightarrow K \cdot {E_A} = 2m{v_o}^2$………eq. (3)
The velocity of the point B is equal to,
$\Rightarrow v = \omega \times R$
$\Rightarrow {v_B} = \omega \times R$
Replacing the value of the angular velocity from equation (1) in the above relation.
$\Rightarrow {v_B} = \omega \times \sqrt 2 \times R$
$\Rightarrow {v_B} = \left( {\dfrac{{{v_o}}}{R}} \right) \times \sqrt 2 \times R$
$\Rightarrow {v_B} = \sqrt 2 \times {v_o}$.
The kinetic energy at point B is equal to,
$\Rightarrow K \cdot {E_B} = \dfrac{1}{2}m{v_B}^2$
Replacing the value of ${v_B}$ we get.
$\Rightarrow K \cdot {E_B} = \dfrac{1}{2}m{\left( {\sqrt 2 {v_o}} \right)^2}$
$\Rightarrow K \cdot {E_B} = \dfrac{2}{2}m{v_o}^2$
$\Rightarrow K \cdot {E_B} = m{v_o}^2$………eq. (4)
The linear velocity of the point C with respect to the ground is zero.
The velocity of point D will be the same as that of point B because of the same radius.
$\Rightarrow {v_D} = \sqrt 2 \times {v_o}$
The kinetic energy of the particle at point D is equal to,
$\Rightarrow K \cdot {E_D} = \dfrac{1}{2}m{v_D}^2$
Replacing the value of velocity at point D we get.
$\Rightarrow K \cdot {E_D} = \dfrac{1}{2}m{v_D}^2$
$\Rightarrow K \cdot {E_D} = \dfrac{1}{2}m{\left( {\sqrt 2 \times {v_o}} \right)^2}$
$\Rightarrow K \cdot {E_D} = \dfrac{2}{2}m{v^2}_o$
$\Rightarrow K \cdot {E_D} = m{v^2}_o$………eq. (5)
Now the kinetic energy of all the particles is equal to,
$\Rightarrow K \cdot E = \dfrac{1}{2}m{v_A}^2 + \dfrac{1}{2}m{v_B}^2 + \dfrac{1}{2}m{v_C}^2 + \dfrac{1}{2}m{v_D}^2$
Replacing the value from equation (3), equation (4) and equation (5) we get.
$\Rightarrow K \cdot {E_P} = \dfrac{1}{2}m{v_A}^2 + \dfrac{1}{2}m{v_B}^2 + \dfrac{1}{2}m{v_C}^2 + \dfrac{1}{2}m{v_D}^2$
$\Rightarrow K \cdot {E_P} = 2m{v_o}^2 + m{v_o}^2 + m{v_o}^2$
$\Rightarrow K \cdot {E_P} = 4m{v_o}^2$………eq. (6)
The kinetic energy due to rotation is equal to,
$\Rightarrow K \cdot {E_R} = \dfrac{1}{2}I{\omega ^2} + \dfrac{1}{2}m{v_o}^2$
$\Rightarrow K \cdot {E_R} = \dfrac{1}{2} \times \left( {m{R^2}} \right) \times {\left( {\dfrac{{{v_o}}}{R}} \right)^2} + \dfrac{1}{2}m{v_o}^2$
$\Rightarrow K \cdot {E_R} = \dfrac{1}{2} \times m \times {v_o}^2 + \dfrac{1}{2}m{v_o}^2$
$\Rightarrow K \cdot {E_R} = m{v_o}^2$………eq. (7)
The total kinetic energy of the ring is equal to,
$\Rightarrow K \cdot {E_T} = K \cdot {E_P} + K \cdot {E_R}$
Replacing from equation (6) and equation (7) we get.
$\Rightarrow K \cdot {E_T} = K \cdot {E_P} + K \cdot {E_R}$
$\Rightarrow K \cdot {E_T} = 4m{v_o}^2 + m{v_o}^2$
$\Rightarrow K \cdot {E_T} = 5m{v_o}^2$.
The total kinetic energy of the ring is equal to $K \cdot {E_T} = 5m{v_o}^2$.

The correct answer for this problem is option C.

Note: It is advisable for the students to remember and understand the formula of the kinetic energy. The kinetic energy of the system will be the combined energy of all the particles of the system. The ring will not be unbalanced as all the four particles are of equal mass and have been symmetrically distributed on the ring.