Question

A ring is suspended at a point on its rim and it behaves as a second’s pendulum, when it oscillates such that its centre moves in its own plane. The radius of the ring would be $(g = {r^2})$
(A) $0.5m$
(B) $1.0m$
(C) $0.67m$
(D) $1.5m$

Answer 1

Hint The time period of a second’s pendulum is $2$seconds. To find the radius of the ring, the ring is considered a physical pendulum. The Moment of inertia and centre of mass of the ring are calculated and are equated with the time period of this physical pendulum, to define its radius.

Complete Step by step solution
It is given in the question that the ring is suspended at a point on its rim and that it oscillates such that the centre moves in its own plane, a diagram of this ring can be drawn as

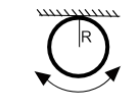
It is given that the ring behaves like a seconds pendulum, therefore the time period of the pendulum,
$T = 2\sec$
For a physical pendulum, time period is given by,
$T = 2\pi \sqrt {\dfrac{I}{{Mg{l_{cm}}}}}$
Where, $I$is the moment of inertia of the pendulum about the axis of its support,
M is the mass of the pendulum
$g$is the acceleration due to gravity
${l_{cm}}$ is the distance of the centre of mass of the pendulum from the point of support.
The centre of mass of a ring is in its centre, since it is suspended from its rim, which means the distance of centre of mass from the support is equal to the radius of the ring, $R$.
${l_{cm}} = R$
The moment of inertia of a ring about its diameter is given by-
${I_{centre}} = M{R^2}$
We require the moment of inertia about its tangent, because this is where it is attached to the support.
Using the parallel axis theorem,
The distance between the axis of diameter and the axis of support is $R$
Therefore,
${I_{\tan }} = M{R^2} + M{R^2} = 2M{R^2}$
Substituting all of these values in the equation for time period,
$2 = 2\pi \sqrt {\dfrac{{2M{R^2}}}{{MgR}}}$
The equation reduces to,
$1 = \pi \sqrt {\dfrac{{2R}}{g}}$
Squaring both sides,
$1 = {\pi ^2}\dfrac{{2R}}{g}$
It is given that $g = {\pi ^2}$,
Therefore,
$2R = 1$
$R = 0.5m$

The radius of the ring is $0.5m$, hence option (A) is correct.

Note Pendulums are of two types, simple and physical, for the simple pendulum the string is massless and bob is assumed to be a point object so that the centre of mass lies at the end of the string. Whereas a physical pendulum can have any shape or size, and can have a different centre of mass and moment of inertia.