Question

A ring is cut from a platinum tube 8.5cm internal and 8.7cm external diameter. It is supported horizontally from the pan of a balance so that it comes in contact with the water in a glass vessel. If an extra $3.97$, if it is required to pull it away from water, then what is the surface tension of water?

Answer 1

In this question, we can find the total force due to the surface tension by using the formula $F = T(2\pi {r_1} + 2\pi {r_2})$. In the formula internal radius and external radius is used but we have given the internal diameter and external diameter in the question. We have to change them into internal radius and external radius. We can find the total force by using $F = mg$.

Complete step by step answer:
According to the question, a ring is cut from the platinum tube having internal diameter ${d_1} = 8.5cm$ and external diameter ${d_2} = 8.7cm$. It is supported in the horizontal position from a pan of a balance which makes it come in contact with water in a glass vessel.

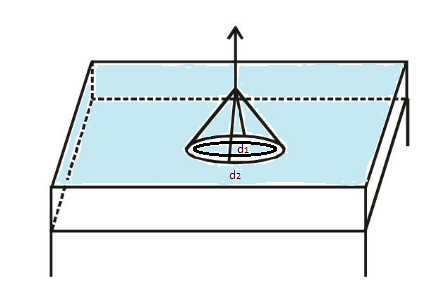
We know that the if $T$ is the surface tension of water, ${r_1}$ is the internal radius and ${r_2}$ is the external radius then total force $F$ due to the surface tension is given by
$F = T(2\pi {r_1} + 2\pi {r_2})$ …………...……………..(i)
Where $2\pi {r_1}$ is the internal circumference and $2\pi {r_2}$ is the external circumference of the ring.
According to the question, an extra mass $m = 3.97g$ is attached with the ring to pull it away from the water then the force is given by-
$F = mg$ ………………………………...(ii)
Where $g$ is the gravitational acceleration is equal to $980cm/{s^2}$ .
So, putting the values of $m$ and $g$in equation (ii), we get-
$F = 3.97 \times 980 \\\ \Rightarrow F = 3890.6dyne \\\$
Noe, let us calculate the internal and external radii of the ring-
${r_1} = \dfrac{{{d_1}}}{2}$
On substituting $d_1$ value,
$\Rightarrow {r_1} = \dfrac{{8.5}}{2}$
On simplification we get,
$\Rightarrow {r_1} = 4.25cm$
And ${r_2} = \dfrac{{{d_2}}}{2}$
On substituting $d_2$ value,
$\Rightarrow {r_2} = \dfrac{{8.7}}{2}$
On simplification we get,
$\Rightarrow {r_2} = 4.35cm$
Now, substituting the value of ${r_1}$, ${r_2}$ and $F$ in the equation (i), we get-
$3890.6 = T(2 \times 3.14 \times 4.25 + 2 \times 3.14 \times 4.35)$
On simplification,
$\Rightarrow T = \dfrac{{3890.6}}{{(2 \times 3.14 \times 4.25 + 2 \times 3.14 \times 4.35)}}$
$\Rightarrow T = \dfrac{{3890.6}}{{(26.69 + 27.32)}}$
On further simplification,
$\Rightarrow T = \dfrac{{3890.6}}{{54.01}}$
$\Rightarrow T = 72.035dyne/cm$

Thus, the surface tension of the water is $72.035dyne/cm$.

Note:
In the question, we can find the surface tension of the water by using the formula of the total force. We can find the internal radius and external radius by using the formula $r = \dfrac{d}{2}$. The unit of mass ($m$) is in C.G.S. So, the value of gravitational acceleration ($g$) will be used $980cm/{s^2}$ or $981cm/{s^2}$. All the units are in C.G.S. So, the unit of surface tension is $dyne/cm$.