Question
Question: A ring has mass \(M\) ,radius \(R\). A point mass \(m\) is placed at a distance \(x\) on the axial l...
A ring has mass M ,radius R. A point mass m is placed at a distance x on the axial line as shown in the figure. Find x so that force experienced is maximum.
A. 3εR
B.2R
C. 2R
D. 3R
Solution
One of the masses is a ring. Consider a small element dm which makes an angle θ with the center of the ring.
dm=2πMdθ
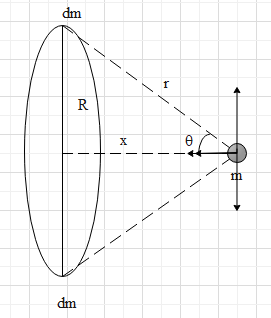
Because of symmetry if we consider two diametrically opposite points. Then the vertical component of forces of both these points on the point mass m will cancel out and the horizontal component gets added up.
The horizontal component is cosθ.
Since, cosθ is equal to adjacent side by hypotenuse,
Here using Pythagoras theorem
Hypotenuse, r=R2+x2
cosθ=R2+x2x
Therefore,
dF=r2G2πMdθm×2×R2+x2x
On integrating we can find F.
When, F is maximum
dxdF=0
Complete step by step answer:
According to the law of gravitation force of gravity is directly proportional to the product of the mass of the bodies and inversely proportional to the square of the distance between them.
In equation form it is given as
F=r2GMm
This is for the case of a point mass.
Here one of the masses is a ring. Let us consider a small element dm which makes an angle θ with the center of the Ring.
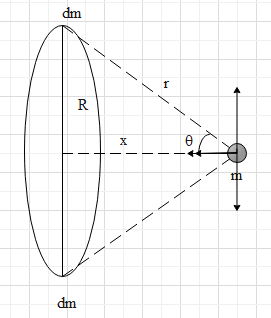
dm=2πMdθ
Because of symmetry if we consider two diametrically opposite points. Then the vertical component of forces of both these points on the point mass m will cancel out and the horizontal component gets added up.
The horizontal component is cosθ.
Since, cosθ is equal to adjacent side by hypotenuse,
cosθ=R2+x2x
Here using Pythagoras theorem
Hypotenuse, r=R2+x2
Therefore,
dF=r2G2πMdθm×2×R2+x2x
Thus,
F=0∫2πr2G2πMdθm=2π(R2+X2)GM2πmR2+x22x
F=(R2+x2)23GMmx
When, F is maximum
dxdF=0 ⇒x×2−3(R2+x2)2−5×2x+(R2+x2)2−3=0 ⇒2x2=R2 ⇒x=2R
So, the correct option is option C.
Note:
- Remember that the equation F=r2GMm is used when both the masses are point masses.
- In this case, one of the masses is a distributed mass. So, we need to modify the equation according to the situation.
- Also, remember that due to the symmetry of the ring if we consider two diametrically opposite points. Then the vertical component of forces of both these points on the point mass m will cancel out and the horizontal component gets added up.
