Question

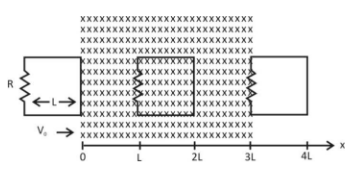
A rigid wire loop of square shape having side length L and resistance R is moving along the x-axis with a constant velocity ${v_0}$ in the plane of the paper. At$t = 0$, the right edge of the loop enters a region of length $3L$ where there is a uniform magnetic field ${B_0}$ into the plane of the paper, as shown in the figure. From sufficiently large ${v_0}$, the loop eventually crosses the region. Let x be the location of the right edge of the loop. Let v(x), I(x) and F(x) represent the velocity of the loop, current in the loop, and force on the loop, respectively, as a function of x. counter-clockwise current is taken as positive.
Which of the following schematic plot(s) is (are) correct? (Ignore gravity)

Answer 1

Recall the concept of motional emf is used and the force through it.Whenever a conducting rod is moving in a magnetic field, either showing translator motion (or) rotatory motions as a result a P.D is established at the ends of the rod. An electric field appears along with the length of the rod directed from the high potential end to the low potential one. This EMF is called Motional EMF.

Formula used:
(i) $i = \dfrac{{VBL}}{R}$
(ii) $F = iLB$
(iii) $F = ma = mv\dfrac{{dv}}{{dx}}$

Complete step by step answer:
Before entering the loop that is before $t = 0$ there is no change in magnetic field and area of loop. So, till $x = 0$no current will flow in the loop. Now, when the loop enters the magnetic field region, its flux changes and hence current is induced in it in counter clockwise direction as given by Fleming’s right hand rule and this current is given by
$i = \dfrac{{VBL}}{R}$… (i). From $x = 0$ to $x = L$
And the force is given by
$F = iLB$
Putting equation (i) in it, we get
$F = \dfrac{{VBL}}{R} \times LB - \dfrac{{V{B^2}{L^2}}}{R}$
This force acts leftward direction while it enters.
When the loop is completely inside the field, there will be no change in flux inside the loop and hence no current will flow through the loop i.e.
From $x = L$to $x = 2L$,
$\Rightarrow i = 0$

Now, again from $x = 2L$ to $x = 3L$, the loop starts moving again and the area changes and current starts flowing again and the force is given by
$F' = - mv\dfrac{{dv}}{{dx}} = \dfrac{{V{B^2}{L^2}}}{R}$
$\Rightarrow dv = - \dfrac{{{B^2}{L^2}}}{{mR}}dx$
Now integrating dv from ${v_0}$ to final velocity v and dx from $0$ to x.
So, we have
$\int\limits_{{v_0}}^v {dv} = \int\limits_0^x {\dfrac{{ - {B^2}{L^2}}}{{mR}}} dx$
$\Rightarrow \left[ v \right]_{{v_0}}^v = \dfrac{{ - {B^2}{L^2}}}{{mR}}\left[ x \right]_0^x$
$\Rightarrow v - {v_0} = \dfrac{{ - {B^2}{L^2}}}{{mR}}x \\\ \Rightarrow {v_0} = \dfrac{{ - {B^2}{L^2}}}{{mR}}x \\\ \Rightarrow v\left( x \right) = {v_0} - \dfrac{{{B^2}{L^2}}}{{mR}}x \\\$
Which is the velocity let $\dfrac{{{B^2}{L^2}}}{{mR}} = K$, a constant. So above equation becomes
$v\left( x \right) = {v_0} - Kx$

Similarly, current is given by

$$I\left( x \right) = L = \dfrac{{VBL}}{R} \\\ \Rightarrow I\left( x \right) = \left[ {{v_0} - \dfrac{{{B^2}{L^2}}}{{mR}}x} \right]\dfrac{{BL}}{R} \\\ \Rightarrow I\left( x \right) = \dfrac{{{v_0}BL}}{R} - \dfrac{{{B^3}{L^3}}}{{m{R^2}}}x \\\ \Rightarrow I\left( x \right) = \dfrac{{{V_0}BL}}{R} - \dfrac{{BLKx}}{R} \\\$$

Now, for $x = 0,{\text{ }}I\left( x \right) = \dfrac{{{v_0}BL}}{R}$
Which is maximum.
And $v\left( x \right) = {v_0} - 0$
$v\left( x \right) = {v_0} =$maximum
So, from $x = 0$to L, I is maximum and V is also maximum i.e.
$\therefore v = {v_0}$
Then b/w $x = L$to $2L$, current becomes zero and v also becomes constant .Then after $x = 2L$, velocity decreases but the current increases.

So, both option B and C are correct.

Note: Remember that as both I and V are functions of x and when the loop is inside the field completely i.e. from $x = L$to $x = 2L$, there will no change in flux hence, no current will flow but it continues to move with constant velocity as for $F = 0,{\text{ a}} = 0$but $v =$constant.