Question

A rigid uniform bar AB of length L is slipping from its vertical position on a frictionless floor (as shown in the figure). At some instant of time, the angle made by the bar with the vertical is $\theta$. Which of the following statements about its motion is/are correct?

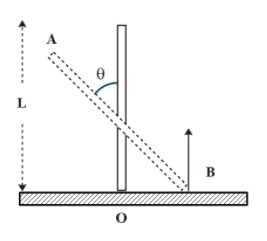
A. The trajectory of the point a is a parabola
B. Instantaneous torque about the point in contact with the floor is proportional to $\sin \theta$
C. The midpoint of the bar will fall vertically downward
D. When the bar makes an angle $\theta$ with the vertical, the displacement of its midpoint from the initial position is proportional to $(1 - \cos \theta )$

Answer 1

We will recreate a rough diagram representing the given system and form components of the forces acting on it and then balance them out. Later we will consider every option and check whether it is correct or not.

Complete answer:
Net force acting upon a body is the vector sum of forces acting on it. Torque is defined as the measure of the force that causes an object to rotate about its axis. The direction of torque depends on the direction of the force on the axis.
Recreating the diagram with the components of forces acting on it we get the following diagram:

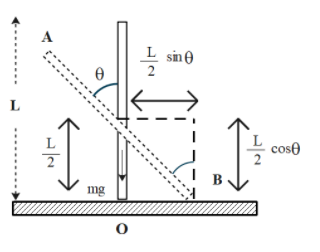
From the figure, the force experienced by the rod is $mg$ in the vertical direction, normal reaction at point B in vertical direction. There is no net force acting in the horizontal direction which means the centre of mass does not move in the horizontal direction. Therefore, the force acting in a vertical direction will move the midpoint of the bar and will fall vertically downward.
Hence, option (C) is correct
Now, let us assume that the distance of point A along the origin horizontally is given by $x$. Similarly, the distance of B from the origin is given by $x$ in the horizontal direction. Then, $\sin \theta = \dfrac{{2x}}{l}$; where $l$ is the length of the rod.
Also, torque upon point B is given by,
$\tau = mg \times \dfrac{l}{2} \times \sin \theta$ = mg \times \dfrac{l}{2} \times \dfrac{{2x}}{l}$= mgx$
$\tau \propto \sin \theta$
Hence, option (B) is correct.
Now, when the bar makes angle zero with the vertical, the distance of the midpoint from the origin is $\dfrac{L}{2}$ and when the bar makes an angle $\theta$ the distance of the midpoint from the origin is $\dfrac{L}{2}\cos \theta$.
Now, displacement of the midpoint from the initial position is $\dfrac{L}{2} - \dfrac{L}{2}{\text{cos}}\theta = \dfrac{L}{2}(1 - {\text{cos}}\theta )$
Hence, option (D) is correct.

Therefore, options (B), (C) and (D) are the correct options for the given question.

Note:
The term net force is used in a system when there is a significant number of forces. Some other forces act on the body when it is either at rest or motion. The net force can accelerate a mass. ${F_{net}} = {F_1} + {F_2} + {F_3}...... + {F_N}$; Where, ${F_1} + {F_2} + {F_3}...... + {F_N}$ is the force acting on the body.