Question

A rigid circular loop of radius $r$ and mass $m$ lies in the $x - y$ plane on a flat table and a current $I$ flowing in it. At this particular place, the magnetic field is $\vec B = {B_x}\hat i + {B_y}\hat j$ . How large $I$ be so that one edge of the loop will lift from the table.
Given $m = 1kg\;$ , $r = 1m\;$ , ${B_x} = 3\;T$ and ${B_y} = 4\;T$ .
(A) $\dfrac{2}{\pi }A$
(B) $\dfrac{\pi }{2}A$
(C) $\dfrac{{10}}{{3\pi }}A$
(D) $\pi A$

Answer 1

To solve this question we consider the given condition in which the wire is placed on the $x - y$ plane and current is flowing through them and the magnetic field is also acting on it. Hence we first evaluate the magnetic moment using the given parameters and then by using the magnetic field and magnetic moment we will find the current flow when one edge of the loop will lift from the table.

Formula used:
Force $\overrightarrow {{\tau _I}}$ acting due to the electric field can be given as
$\Rightarrow \overrightarrow {{\tau _I}} = \vec M \times \vec B$
Where $\vec M$ is the magnetic moment and $\vec B$ is the magnetic field.
The magnetic moment of a substance
$\Rightarrow \vec M = I \times A$
Where $I$ is the component of current and $A$ is area.

Complete Step-by-step solution
Here given that the circular rigid wire is placed on the $x - y$ plane having radius $r$ and mass $m$ and the current $I$ is passing through it. The wire is lifted by its one end from the table. The diagram of this arrangement is given as

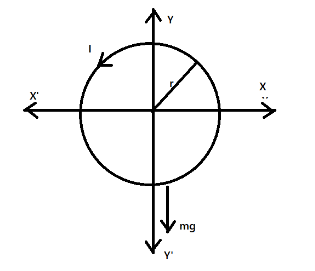
Hence from the diagram, it can be evaluated that when the wire is lifted from the table from its one end then a force $m\;g$ is acting on the other end in the downward direction which can be given as $\overrightarrow {{\tau _I}}$
$\Rightarrow \overrightarrow {{\tau _I}} = \vec M \times \vec B$ ………. $(1)$
Where $\vec M$ is the magnetic moment and $\vec B$ is the magnetic field.
The magnetic moment of a substance can be evaluated as
$\Rightarrow \vec M = I \times A\hat k$ ……… $(2)$
Now the area of the circular loop is given as
$\Rightarrow A = \pi {r^2}$ ……… $(3)$
Substitute the values of the equation $(2)$ and $(3)$ in the equation $(1)$ , hence
\Rightarrow \overrightarrow {{\tau _I}} = \left\\{ {\pi {r^2}I\hat k} \right\\} \times {B_x}\hat i + {B_y}\hat j
\Rightarrow \overrightarrow {{\tau _I}} = \left| {\begin{array}{*{20}{c}} {\hat i}&{\hat j}&{\hat k} \\\ 0&0&{\pi {r^2}I} \\\ {{B_x}}&{By}&0 \end{array}} \right|
Hence evaluating the determinant of the matrix we get
$\Rightarrow \overrightarrow {{\tau _I}} = \hat i\left( {0 - {B_y}I\pi {r^2}} \right) - \hat j\left( {0 - {B_x}I\pi {r^2}} \right)$
$\Rightarrow \overrightarrow {{\tau _I}} = I\pi {r^2}\left( {\hat j{B_x} - \hat i{B_y}} \right)$
Now evaluating the magnitude of the current
$\Rightarrow \overrightarrow {{\tau _I}} = I\pi {r^2}\sqrt {{B_x}^2 + {B_y}^2}$
$\Rightarrow mg = I\pi {r^2}\sqrt {{B_x}^2 + {B_y}^2}$
Upon rearranging the equation we get,
$\Rightarrow I = \dfrac{{mg}}{{\pi {r^2}\sqrt {{B_x}^2 + {B_y}^2} }}$
Substituting the values of $r = 1m\;$ , ${B_x} = 3\;T$ and ${B_y} = 4\;T$ , and $m = 1\;kg$
$\Rightarrow I = \dfrac{{1 \times 10}}{{\pi {{\left( 1 \right)}^2}\sqrt {{{\left( 3 \right)}^2} + {{\left( 4 \right)}^2}} }}$
$\therefore I = \dfrac{2}{\pi }A$
Hence the electric current acting when one edge of the loop will lift from the table is $I = \dfrac{2}{\pi }A$ .
Therefore option (A) is the correct answer.

Note
While dealing with vector quantities always ensure the direction of the components given. In this question for multiplication, we have used the matrix representation of the quantities. Also, ensure to use the correct units while dealing with a large number of parameters.