Question

A rigid body moves a distance of 10 m along a straight line under the action of a force 5N. If the work done by this force on the body is 25 joules, the angle which the force makes with the direction of motion of the body is
$\begin{aligned} & \text{A}\text{. }{{\text{0}}^{0}} \\\ & \text{B}\text{. 3}{{\text{0}}^{0}} \\\ & \text{C}\text{. 6}{{\text{0}}^{0}} \\\ & \text{D}\text{. 9}{{\text{0}}^{0}} \\\ \end{aligned}$

Answer 1

To solve this question first obtain the component of the force acting on the body in the direction of the motion of the body. Then put these values on the equation for work done to find the angle between the force and the direction of motion of the body.

Complete step-by-step answer:

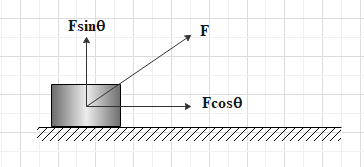
Let, the force F acting on the box makes an angle $\theta$ with the direction of motion of the box. Breaking the force into its components, the component of the force along the direction of motion of the box is $F\cos \theta$ and the component of force acting along the perpendicular direction of the direction of motion of the box is $F\sin \theta$ .
Now, the work done by a force can be expressed as the product of the force in the direction of motion and the distance covered by the object under the force. Mathematically we can express it as,
$W=FS\cos \theta$
Here, the force on the box is 5 N.
So, the component of force in the direction of motion of the box will be $5\cos \theta \text{ N}$ .
The distance covered by the object in the direction of motion is 10m.
Given, the work done by the force on the object is 25 joules.
Putting these values on the above equation, we get that,
$\begin{aligned} & W=FS\cos \theta \\\ & 25=5\times 10\cos \theta \\\ & 25=50\cos \theta \\\ & \cos \theta =\dfrac{25}{50} \\\ & \cos \theta =\dfrac{1}{2} \\\ & \theta ={{\cos }^{-1}}\left( \dfrac{1}{2} \right) \\\ & \theta ={{60}^{0}} \\\ \end{aligned}$
So, the force acting on the body makes an angle of ${{60}^{0}}$ with the direction of motion of the body.
The correct option is (C).

Note: Work done given by the dot product of the force applied on the object and displacement of the object. We can mathematically express it as,
$W=\vec{F}.\vec{S}=FS\cos \theta$
Where $\theta$ is the angle between the force and the direction of motion of the object.