Question

A rigid body in the shape of a V has two equal arms made of uniform rods. What must be the angle between the two roads so that when the body is suspended from one end the other arm is horizontal?
A. ${\cos ^{ - 1}}\left( {\dfrac{1}{3}} \right)$
B. ${\cos ^{ - 1}}\left( {\dfrac{1}{2}} \right)$
C. ${\cos ^{ - 1}}\left( {\dfrac{1}{4}} \right)$
D. ${\cos ^{ - 1}}\left( {\dfrac{1}{6}} \right)$

Answer 1

For solving this question, we can consider an isosceles triangle with the V-shaped body forming the equal sides of the triangle. The center of mass will be along the vertical line from the hinge. A line drawn from the vertex of the V-shaped body towards the base of the triangle will be the angle bisector and it will form the altitude of the isosceles triangle. A line drawn parallel to the base through the center of mass will cut the equal sides at the midpoint. Using this information, we can find the value of the angle between the rods.

Complete step by step answer:
Consider the diagram shown below of the V-shaped body hanging from one end.

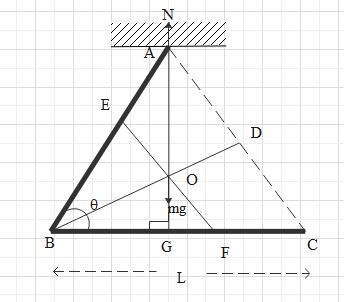
It is given that a V shaped rod has 2 arms made of uniform rods.
We are asked to find the angle between the rods when the body is suspended from one end such that the other end is horizontal.
When the other end is horizontal let the system be at equilibrium.
At equilibrium, the centre of mass will be lying on the vertical line drawn from the hinge.
The hinge will provide the normal force to balance the weight $mg$ acting downwards.
If we join the endpoints of V then we will get an isosceles triangle which is a triangle with two sides and two angles equal.
Consider a line joining the vertex of the V-shaped body through the centre of mass of the body to the base of the triangle formed.
This line will be the angle bisector.
Since the triangle is an isosceles triangle.
The angles,
$\angle ACB = \angle CAB$
In an isosceles triangle, the angle bisector will be the altitude.
Thus, the line BD is normal to side CA.
If we consider a line EF parallel to side AC through the centre of mass. Then
$\angle EOB = {90^0}$
Since it is the corresponding angle to $\angle BDA$ which is ${90^ \circ }$.
We know that the line through the centre of mass parallel to the base will cut the equal sides of the isosceles triangle in the ratio $2:1$. But since the third side is not present here the centre of mass will be slightly raised towards the vertex of equal sides. So, the line parallel to the base of the triangle through the centre of mass will cut the sides in the ratio $1:1$.
So the line EF will cut the side $AB$ and $BC$ into 2 equal halves of length $\dfrac{L}{2}$
Now consider triangle ABG.
We know,
$\cos \theta = \dfrac{{{\text{adjacent}}\,{\text{side}}}}{{{\text{Hypotenuse}}}} = \dfrac{{AG}}{{AB}}$
$\Rightarrow AG = AB\cos \theta = L\cos \theta$
Now consider the triangle BOG
$\cos \dfrac{\theta }{2} = \dfrac{{BG}}{{GO}}$
$\Rightarrow \cos \dfrac{\theta }{2} = \dfrac{{L\cos \theta }}{{\dfrac{L}{2}\cos \dfrac{\theta }{2}}}$
$\Rightarrow {\cos ^2}\dfrac{\theta }{2} = 2\cos \theta$
$\Rightarrow \dfrac{{1 + {{\cos }^2}\left( {2\dfrac{\theta }{2}} \right)}}{2} = 2\cos \theta$
$\Rightarrow l + \cos \theta = 4\cos \theta$
$\Rightarrow \cos \theta = \dfrac{1}{3}$
$\therefore \theta = {\cos ^{ - 1}}\left( {\dfrac{1}{3}} \right)$
This is the angle between the two rods when one side is horizontal.

Therefore, the correct answer is option A.

Note:
Here remember that the centre of mass is not at the exact centre of the triangle. We considered the sides of V as the 2 equal sides. The third side is absent. So, the centre of mass will be slightly raised towards the vertex of the V shaped body from the centre. If there was actually a third side the line through the centre of mass parallel to base will cut the equal sides of the isosceles triangle in the ratio $2:1$. But since the third side is not present the line parallel to the base of the triangle through the centre of mass will cut the sides in the ratio $1:1$.