Question
Question: A right triangular plate ABC of mass \(m\)is free to rotate in the vertical plane about a fixed hori...
A right triangular plate ABC of mass mis free to rotate in the vertical plane about a fixed horizontal axis through A. It is supported by a string such that the side AB is horizontal. The reaction at the support A is:
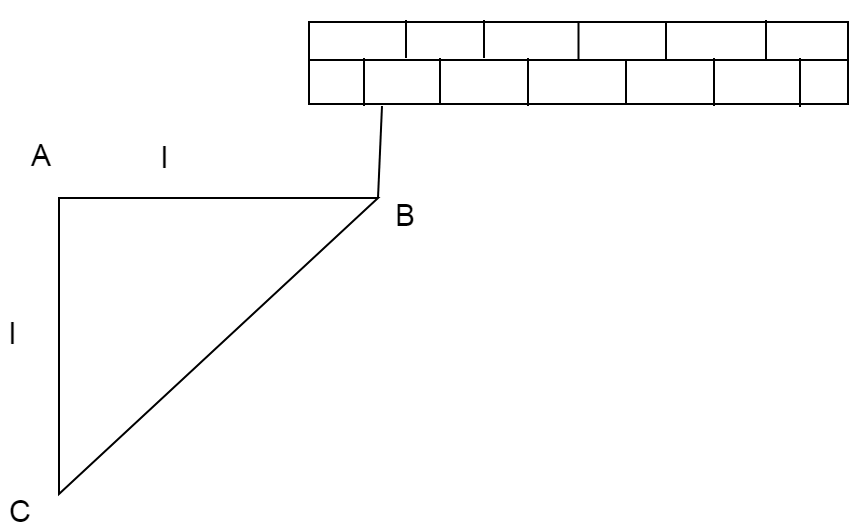
(A) 3mg
(B) 32mg
(C) 2mg
(D) mg
Solution
In order to solve this question, we need to use the concept of centroid as it is the point at which the entire mass of the system is balanced. Now we need to find the force experienced at point A. Now, Taking moment of force around point B, we can obtain the required solution.
Complete Step-By-Step solution:
We know that the length AB given to us is l.
We know that, in the case of a right angled triangle, the centroid lies at a distance of 32od the base, in this case it is l.
Now, let us consider that at any point in the given system the torque is conserved. Suppose we consider the torque to be conserved at point B.
Now, the tension due to the string acts at point B as well.
Now, we know that torque is the product of force and its perpendicular distance. Thus, at point B torque is 0as the perpendicular distance is0.
We know that point A acts as a support, therefore, an upward normal force must exist acting at the distancel.
Let us consider this force asN.
Now, this normal force is opposed by the weight of the body which acts from the centroid.
Thus, the total torque at A is given by:
N×l−mg×32l
Where, mis the mass of the plate
Now, since the total torque is conserved, we can write:
N×l−mg×32l=0
On solving the equation and cancelling the equal terms, we get:
N=32mg
This is our required solution.
Hence, option (B) is correct.
Note:
Centroid of a triangle implies the point where three medians intersect. This can be computed using the coordinates of three points that makes the triangle. The centre of mass of a triangle lies at its centroid. This is thus the point where the entire weight of the triangle can be balanced.
