Question
Question: A right isosceles triangle of side \(a\) has charges \(q, + 3q\) and \( - q\) arranged on its vertic...
A right isosceles triangle of side a has charges q,+3q and −q arranged on its vertices as shown in figure. What is the electric potential at P midway between the line connecting the +q and −q charges?
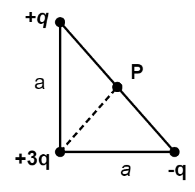
A. rε0a3q
B. 2πε0a3q
C. πε0aq
D. 22πε0a3q
Solution
Use the superposition principle, to find the electric potential at a point in a system with multiple charges. Use the known geometrical relationships to find the distances between the charges and the point.
Complete step by step answer:
Let us first label the points in the diagram, to refer to them easily while using geometrical relationships.
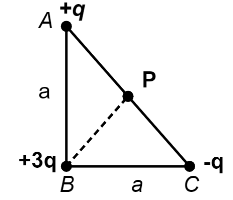
We are asked to find the electric potential at the point P due to the charges +q,−q and +3q. We will first find out the potential at P due to a single charge and then use the superposition principle to find the collective electric potential at P. And for this we need to know the distances AP,BP,CP.
We are given that △ABC is a right-angled triangle and point P is the midpoint of AC. So, by using Pythagoras theorem we have, AC=2a and AP=PC=2a. We can also observe that △ABP≅△CBP [by SSS congruence criterion]. And so, ∠ABP=∠CBP=45∘. Also, since △ABC is isosceles we have ∠A=∠C=45∘. Now since, sides opposite to opposite angles are equal, in △ABP, we have AP=BP=2a [because ∠ABP=∠BAP=45∘].
So, we now know the distances between the charges and the point P;
AP=BP=CP=2a
So, the electric potential at P due to +q is,
V1=4πε02aq=22πε0aq
Electric potential at P due to −q is,
V2=4πε02a−q=22πε0a−q
And, electric potential at P due to +q is,
V3=4πε02a3q ⇒V3=22πε0a3q
We know from the superposition of electric potential that the electric potential of a system of charges is the sum of potentials of the individual charges.
So, the electric potential at P V=V1+V2+V3.
V=22πε0aq+22πε0a−q+22πε0a3q
∴V=22πε0a3q
Hence, the answer is option D.
Note: The electric potential at a point is the amount of work which is needed to move a charge from a reference point to that point. Usually, we consider the reference point at infinity. Whereas, potential difference between two points is the amount of work that needs to be done to bring a charge from one point to the other.
