Question

A right circular cylindrical tower height $h$ and radius $r$ stands on the ground. Let $P$ be a point in the horizontal plane ground and ABC are the semicircular edge of the top of the tower such that B is the point in it nearest to $P$ . The angles of elevation of the points A and B are 45° and 60° respectively. Show that $\dfrac{h}{r} = \dfrac{{\sqrt 3 \left( {1 + \sqrt 3 } \right)}}{2}$.

Answer 1

We will draw a figure to represent the situation given in the question. We will find the value of $h$ and $r$ using standard trigonometric ratios. We will compute $\dfrac{h}{r}$ and simplify the equation to get the desired form.

Formulas used:
In a right angled triangle $\tan \theta = \dfrac{P}{B}$ where $P$ is the perpendicular of the triangle and $B$is the base of the triangle.
$\tan {60^ \circ } = \sqrt 3$
$\tan {45^ \circ } = 1$
$\left( {a - b} \right)\left( {a + b} \right) = {a^2} - {b^2}$

Complete step-by-step answer:
We will draw a figure for the question:

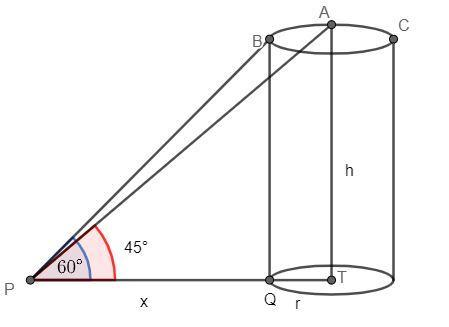
Both $AT$ and $BQ$ have length $h$.
We will assume that the length of $PQ$is $x$.
In $\Delta BPQ$, $BQ$ is the perpendicular and $PQ$ is the base. We will use the first and second formula to find $\dfrac{h}{x}$ :
$\begin{array}{c}\tan {60^ \circ } = \dfrac{{BQ}}{{PQ}}\\\\\tan {60^ \circ } = \dfrac{h}{x}\\\\\left( 1 \right){\rm{ }}\sqrt 3 = \dfrac{h}{x}\end{array}$
We can see from the figure that $PT = x + r$
In $\Delta PAT$, $AT$is the perpendicular and $PT$is the base. We will use the first and third formula to find $x$:
$\tan {45^ \circ } = \dfrac{{AT}}{{PT}}\\\\\Rightarrow \tan {45^ \circ } = \dfrac{h}{{x + r}}\\\ \Rightarrow 1 = \dfrac{h}{{x + r}}\\\x + r = h\\\\\Rightarrow \left( 2 \right){\rm{ }}x = h - r$
We will substitute $h - r$ for $x$ in the first equation:
$\sqrt 3 = \dfrac{h}{{h - r}}$
We will cross multiply $h - r$ with $\sqrt 3$ :
$\Rightarrow \sqrt 3 \left( {h - r} \right) = h\\\\\Rightarrow \sqrt 3 h - \sqrt 3 r = h\\\ \Rightarrow \sqrt 3 h - h = \sqrt 3 r\\\ \Rightarrow h\left( {\sqrt 3 - 1} \right) = \sqrt 3 r\\\ \Rightarrow \dfrac{h}{r} = \dfrac{{\sqrt 3 }}{{\sqrt 3 - 1}}$
We will multiply the numerator and the denominator in the right-hand side with$\left( {\sqrt 3 + 1} \right)$ to convert the denominator into rational form:
$\Rightarrow \dfrac{h}{r} = \dfrac{{\sqrt 3 \left( {\sqrt 3 + 1} \right)}}{{\left( {\sqrt 3 - 1} \right)\left( {\sqrt 3 + 1} \right)}}$
We will substitute $\sqrt 3$ for $a$ and 1 for $b$ in the 4th formula:
$\Rightarrow \begin{array}{l}\dfrac{h}{r} = \dfrac{{\sqrt 3 \left( {\sqrt 3 + 1} \right)}}{{{{\left( {\sqrt 3 } \right)}^2} - 1}}\\\ \Rightarrow \dfrac{h}{r} = \dfrac{{\sqrt 3 \left( {\sqrt 3 + 1} \right)}}{2}\end{array}$
$\therefore$ We have shown that $\dfrac{h}{r} = \dfrac{{\sqrt 3 \left( {\sqrt 3 + 1} \right)}}{2}$.
Note: We can also find the solution by cross multiplying $x$ with $\sqrt 3$ in the 1st equation:
$\begin{array}{c}\sqrt 3 x = h\\\x = \dfrac{h}{{\sqrt 3 }}\end{array}$
We will substitute $\dfrac{h}{{\sqrt 3 }}$ for $x$ in the 2nd equation:
$\Rightarrow \dfrac{h}{{\sqrt 3 }} = h - r\\\ \Rightarrow \dfrac{h}{{\sqrt 3 }} - h = r\\\h\left( {\dfrac{1}{{\sqrt 3 }} - 1} \right) = r$
We will take the L.C.M.:
$\Rightarrow h\left( {\dfrac{{1 - \sqrt 3 }}{{\sqrt 3 }}} \right) = r\\\\\Rightarrow \dfrac{h}{r} = \dfrac{{\sqrt 3 }}{{1 - \sqrt 3 }}$
We will multiply the numerator and the denominator in the right-hand side with$\Rightarrow \left( {\sqrt 3 + 1} \right)$ to convert the denominator into rational form:
$\Rightarrow \dfrac{h}{r} = \dfrac{{\sqrt 3 \left( {\sqrt 3 + 1} \right)}}{{\left( {\sqrt 3 - 1} \right)\left( {\sqrt 3 + 1} \right)}}$
We will substitute $\sqrt 3$ for $a$ and 1 for $b$ in the 4th formula:
$\Rightarrow \dfrac{h}{r} = \dfrac{{\sqrt 3 \left( {\sqrt 3 + 1} \right)}}{{{{\left( {\sqrt 3 } \right)}^2} - 1}}\\\\\Rightarrow \dfrac{h}{r} = \dfrac{{\sqrt 3 \left( {\sqrt 3 + 1} \right)}}{2}$
We have proven the desired result.