Question

A right-angled tube is fixed horizontally on a horizontal surface and an ideal liquid of density $p$ is flowing into the tube at the rate of $Q = 4{m^3}/s$. Cross-sectional areas of the tube at intake and outlet positions are $A = 2{m^2}$ and $S = 1{m^2}$ respectively. The magnitude of the net force exerted by the liquid on the tube is (Given that the value of atmospheric pressure ${P_0} = 4pN/{m^2}$)
A) $3\sqrt {12} p$
B) $4\sqrt {41} p$
C) $5\sqrt {21} p$
D) None of the above

Answer 1

The pressure is the amount of force exerted per unit area. This pressure difference causes fluid to flow from a low-pressure region to a high-pressure region. The pressure is only considered from the amount of thrust or the perpendicular force applied by the fluid in the area. The other components are not considered anyway.

Complete step by step solution:
Given:
The rate of the flow in the tube is $Q = 4{m^3}/s$ in the first half of its running time.
The intake cross-section is $A = 2{m^2}$ and the outlet cross-section is $S = 1{m^2}$.
The atmospheric pressure is ${P_0} = 4pN/{m^2}$
We need to find the net force exerted by the liquid on the pipe.

Step 1:

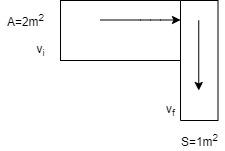
The mass of the amount of liquid passing through the pipe at any instance is $m = pQ$.
Now if the liquid in the pipe has an initial velocity of ${v_i}$ and a final velocity of ${v_f}$, then you can calculate the net exerted force by the liquid from the rate of change of momentum.
$\therefore {F_{Net}} = pQ \times \left( {{v_f} - {v_i}} \right)$

Step 2:
Now the pipe is given to be perpendicular, so the effect of the two perpendicular components of forces can not affect each other. Hence they should be treated separately.
The pressure of a liquid is calculated from the perpendicular force per the thrust exerted by the liquid.
So, for the horizontal side of the pipe, only the $x$ component of the force is effective.
Else in the opening end, atmospheric pressure comes into play.
You can compute the initial velocity ${v_i}$ of the liquid as the rate of the liquid flowing per area, that is ${v_i} = \dfrac{Q}{A}$.
The end of the horizontal side denotes the start of the flow in $y$ direction completely, hence ${v_f} = 0$.
Let the liquid exert a force ${F_x}$.
So, balancing the forces to keep the system in equilibrium you can write
${P_0}A - {F_x} = Qp\left( {0 - \dfrac{Q}{A}} \right) \\\ \Rightarrow 4p \times 2 - {F_x} = 4 \times p \times \left( {0 - \dfrac{4}{2}} \right) \\\ \Rightarrow 8p - {F_x} = - 8p \\\ \Rightarrow {F_x} = 16p \\\$

Step 3:
Similarly, for the vertical side of the pipe, only the $y$ component of the force is effective.
In the opening end, atmospheric pressure comes into play.
The end of the horizontal side denotes the start of the flow in $y$direction completely, hence in this case ${v_i} = 0$.
You can compute the final velocity ${v_f}$ of the liquid as the rate of the liquid flowing per area, which is ${v_f} = \dfrac{Q}{S}$.
Let the liquid exert a force ${F_y}$.
So, balancing the forces to keep the system in equilibrium you can write
${F_y} - {P_0}S = Qp\left( {\dfrac{Q}{S} - 0} \right) \\\ \Rightarrow {F_y} - 4p \times 1 = 4 \times p \times \left( {\dfrac{4}{1} - 0} \right) \\\ \Rightarrow {F_y} + 4p = 16p \\\ \Rightarrow {F_y} = 20p \\\$
Step 4:
Hence you get the $x$ component of the force as ${F_x} = 16p$ and the $y$ component of the force as ${F_y} = 20p$.
Compute the magnitude of the net force from the two components
${F_{Net}} = \sqrt {{F_x}^2 + {F_y}^2} \\\ = \sqrt {{{\left( {16p} \right)}^2} + {{\left( {20p} \right)}^2}} \\\ = \sqrt {256{p^2} + 400{p^2}} \\\ = \sqrt {656{p^2}} \\\ = \sqrt {4 \times 4 \times 41} p \\\ = 4\sqrt {41} p \\\$
$\therefore {F_{Net}} = 4\sqrt {41} p$

The magnitude of net force exerted by liquid on the tube is $4\sqrt {41} p$. Hence, option (B) is correct.

Note:
Only the perpendicular forces on the cross-section are considered to compute the pressure. So, you need to resolve the force into two components along with the orientation of the pipe. For this type of case, the velocity should be calculated only in the ends because in the middle of the fluid that is variable everywhere. Here, the pipe is rectangular, and hence the resolution is two perpendicular components but for any general shape of the pipe, you should carefully consider the angle while resolving the components.