Question

A right-angled prism of apex angle 4° and refractive index 1.5 is located in front of a vertical plane mirror as shown in the figure. A horizontal ray of light is falling on the prism. Find the total deviation produced in the light ray as it emerges 2nd time from the prism.

(A) 8° CW
(B) 6° CW
(C) 180° CW
(D) 174° CW

Answer 1

Hint : A ray of light entering a material with refractive index more than one gets deflected from its original path due to refraction. The deviation produced in the light ray due to refraction caused by prism is directly related to its refractive index value and apex angle.

Complete Step By Step Answer:
In order to find the total deviation produced in the ray of light due to right-angled prism, it is given to us that:
The apex angle of the prism is $A^\circ = 4^\circ$
The refractive index of the prism is $\mu = 1.5$
Then, we can find the angle of deviation $\delta$ in the ray of light due to prism using the formula, $\delta = \left( {\mu - 1} \right)A^\circ$

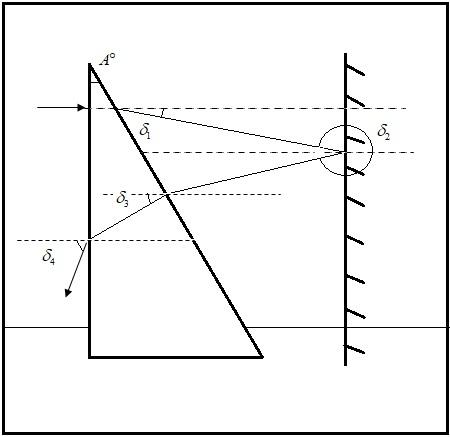
As the ray of light emerges from the right-angled prism, it undergoes its first deviation. Let us name it as ${\delta _1}$ , such that on substituting the values of apex angle and refractive index, we get:
${\delta _1} = \left( {1.5 - 1} \right)4^\circ$
$\Rightarrow {\delta _1} = 0.5 \times 4^\circ$
$\Rightarrow {\delta _1} = 2^\circ CW$
This means that the light ray emerging out of the prism undergoes a deviation of $2^\circ$ in clockwise direction from its original path, due to refraction.
Now, as the ray of light encounters the mirror it gets reflected. And according to Snell’s law we know that angle of incidence is equal to angle of reflection. Thus,
${\delta _1} = \angle i = \angle r = 2^\circ CW$
The ray of light experiences second deflection due to mirror given by reflex angle as,
${\delta _2} = \pi - 2{\delta _1}$
$\Rightarrow {\delta _2} = 180^\circ - 2 \times 2^\circ$
$\Rightarrow {\delta _2} = 176^\circ CW$
Thus, the ray of lilght further gets deflected by $176^\circ$ in clockwise direction.
Now, the ray of light will again enter the prism and experiences a deviation due to refraction, such that:
${\delta _3} = \left( {1.5 - 1} \right)4^\circ$
$\Rightarrow {\delta _3} = 2^\circ ACW$
It gets $2^\circ$ deviated in an anti-clockwise direction.
As, the ray of light finally emerges out of the prism, it undergoes on last deviation, that is
${\delta _4} = \left( {1.5 - 1} \right)4^\circ$
$\Rightarrow {\delta _4} = 2^\circ ACW$
So, the emergent ray is also $2^\circ$ deviated in an anticlockwise direction.
Then the total angle of deviation in the ray of light is:
${\delta _{total}} = {\delta _1} + {\delta _2} + {\delta _3} + {\delta _4}$
$\Rightarrow {\delta _{total}} = 2^\circ + 176^\circ - 2^\circ - 2^\circ$
$\Rightarrow {\delta _{total}} = 2^\circ + 176^\circ - 2^\circ - 2^\circ$
$\Rightarrow {\delta _{total}} = 174^\circ CW$
Thus, the total deviation angle of the light ray is $174^\circ$ from its original path and in the clockwise direction.
Hence, option (D) is correct.

Note :
If a ray of light undergoes multiple changes in its path, then the sum of these deflections is known as the total deviation angle of the light ray. The clockwise (CW) direction is considered positive in nature and the anti-clockwise (ACW) direction is considered negative in nature.