Question
Question: A right-angled prism made from a material of refractive index \(\mu \) is kept in air. A ray PQ is i...
A right-angled prism made from a material of refractive index μ is kept in air. A ray PQ is incident normally on the side AB of the prism. Find (in terms of μ ) the maximum value of θ up to which this incident ray necessarily undergoes total internal reflection at the face AC of the prism.
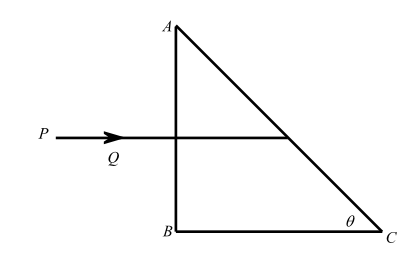
Solution
In this question, we know that if the angle between two lines is the same as the angle between their perpendiculars and one angle of right angles prism is always 90∘. The angle of incidence should be minimum for total internal reflection.
Complete step by step solution:
In this question we have given that a right-angled prism has the refractive index μ. We need to calculate the maximum value of θ up to which this incident ray necessarily undergoes total internal reflection at the face AC of the prism.
In this question let us assume that the angle of incidence is i and the angle of incidence is incident on AC.
The angle between two lines is same as the angle between their perpendiculars so we can write,
i=A
Since the prism is right angled, we can write,
⇒θ=2π−A
Since i=A we can write,
⇒θ=2π−i......(1)
We know that refractive index is expressed as,
μ=sini1
As we know that the angle of incidence should be minimum for the total internal reflection,
ic=sin−1μ1......(2)
Here, ic is a critical angle.
Now the maximum value of θ for total internal expression can be calculated by substituting the expression of ic to the equation (1) as,
⇒θ=2π−iC
Now we substitute the value of critical angle as expressed in equation (2) in above equation to get the maximum value of θ.
∴θmax=2π−sin−1μ1
Therefore, the maximum value will be θmax=2π−sin−1μ1.
Note: As we know that the minimum angle for total internal reflection is the critical angle. The angle of the right-angled prism is 90∘. The maximum value of θ is calculated corresponding to the minimum value of i.
