Question
Question: A revolver of mass \({m_r}\) fires a bullet of mass \({m_b}\) in a free space. The bullet is hit a r...
A revolver of mass mr fires a bullet of mass mb in a free space. The bullet is hit a resting block mass mr at a distance S away from the revolver. Distance travelled by the centre of mass of the bullet and block system when the bullet travels through a distance x towards the block is:
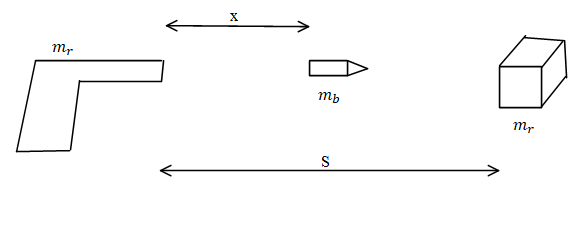
A) mr+mbmbx.
B) mr+mbmbx+mrs.
C) mr+mbmr(s−x).
D) All of the above
Solution
The centre of mass of a system is the point where the mass of the whole system can be assumed to be concentrated. Whenever the bullet is fired by the rifle then the rifle moves a bit back side because of the recoil.
Formula used:
The momentum of any body is equal to,
⇒p=m×v
Where mass is m and velocity is v.
Complete step by step solution:
It is given in the problem that a revolver of mass mrfires a bullet of mass mb in a free space the bullet is a hit a resting block mass mr at a distance S away from the revolver and we need to find the distance travelled by the centre of mass of the bullet and block system when the bullet travels through a distance x towards the block.
The centre of mass system before the bullet is fired is given by,
⇒Xcom=mr+mbmr×0+(mb×s)
⇒Xcom=mr+mbmr×0+(mb×s)
⇒Xcom=mr+mbmb×s………eq. (1)
The centre of mass of the system after the bullet is fired.
⇒Xcom=mr+mb(mr×0)+mb×(s−x)
⇒Xcom=mr+mbmb×(s−x)………eq. (2)
Let d be the distance travelled by the centre of mass.
Subtracting equation (1) by equation (2) we get,
⇒d=mr+mbmb×s−mr+mbmb×(s−x)
⇒d=mr+mb(mb×s)−mb×(s−x)
⇒d=mr+mb(mb×s)−(mb×s)+(mb×x)
⇒d=mr+mb(mb×x).
Option A is the correct answer for this problem.
Note: The students are advised to remember the formula of the centre of the mass as it is very useful in solving the problem like these. The position of the block does not change in both the cases but the bullet moves a distance x.
