Question

A rests against a wall at an angle $\alpha$ to the horizontal. Its foot is pulled away from the wall through a distance a, so that it slides a distance b down the wall making an angle $\beta$ with the horizontal, show that
$a=b\tan \dfrac{1}{2}\left( \alpha +\beta \right)$

Answer 1

To solve this question, firstly we will draw the figure according to the question. Take we will take the length of the ladder same for both conditions mentioned. From the two triangles formed find the value of sine and cosine function. Thus we will find the length of sides and get the equation connecting $\dfrac{a}{b}$ sing the trigonometric identities to prove the expression such as $\dfrac{\sin \theta }{\cos \theta }=\tan \theta$, $\sin \alpha =\dfrac{perpendicular}{hypotenuse}$ and $\cos \alpha =\dfrac{base}{hypotenuse}$.

Complete step-by-step answer:
Consider the figure that is drawn.
Let AB be the wall against which the ladder is laid.

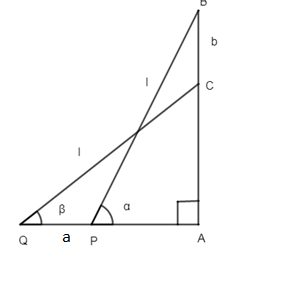
Let PB be the first position where the ladder was laid.
Let PB = l, where l is the length of the ladder.
The ladder makes angle $\alpha$ with the wall AB.
So, QC = l.
Now ladder makes angle $\beta$ with the wall AB.
The wall is perpendicular to the ground. So, $AB\bot QA$.
So we have been told to take that distance as b. The foot of the ladder is pulled away from point P to point Q. Thus the distance QP can be marked as a.
Now let us first consider, $\Delta PAB$, right angled at A.
$\therefore \sin \alpha$ = opposite side / hypotenuse $=\dfrac{AB}{PB}$

& \sin \alpha =\dfrac{AB}{l} \\\ & \therefore AB=l\sin \alpha \\\ \end{aligned}$$ Similarly, $$\cos \alpha $$ = adjacent side / hypotenuse $$=\dfrac{AP}{PB}$$ $$\begin{aligned} & \cos \alpha =\dfrac{AP}{l} \\\ & \therefore AP=l\cos \alpha \\\ \end{aligned}$$ Now let us consider, $$\Delta QAC$$. $$\sin \beta $$ = opposite side / hypotenuse $$=\dfrac{AC}{QC}$$ $$\begin{aligned} & \sin \beta =\dfrac{AC}{l} \\\ & \Rightarrow AC=l\sin \beta \\\ \end{aligned}$$ Similarly, $$\cos \beta $$ = adjacent side / hypotenuse $$=\dfrac{AQ}{QC}$$ $$\therefore AQ=l\cos \beta $$ Thus we know that, $$AB=l\sin \alpha ,AP=l\cos \alpha $$ $$AC=l\sin \beta ,AQ=l\cos \beta $$ We know, AB = AC + BC $$\therefore $$ BC = AB – AC $$=l\sin \alpha -l\sin \beta $$ BC = b [From the figure] $$\therefore b=l\left( \sin \alpha -\sin \beta \right)-(1)$$ Similarly, AQ = AP + PQ PQ = AQ – AP $$=l\cos \beta -l\cos \alpha $$ PQ = a [From figure] $$\therefore a=l\left( \cos \beta -\cos \alpha \right)-(2)$$ Now let us find $$\dfrac{a}{b}$$ i.e. Equation (2) / Equation (1). $$\begin{aligned} & \therefore \dfrac{a}{b}=\dfrac{l\left( \cos \beta -\cos \alpha \right)}{l\left( \sin \alpha -\sin \beta \right)} \\\ & \therefore \dfrac{a}{b}=\dfrac{\cos \beta -\cos \alpha }{\sin \alpha -\sin \beta }=\dfrac{-\left( \cos \alpha -\cos \beta \right)}{\sin \alpha -\sin \beta } \\\ \end{aligned}$$ We know the trigonometric identities, $$\begin{aligned} & \cos a-\cos b=-2\sin \left( \dfrac{a+b}{2} \right)\sin \left( \dfrac{a-b}{2} \right) \\\ & \sin a-\sin b=2\cos \left( \dfrac{a+b}{2} \right)\sin \left( \dfrac{a-b}{2} \right) \\\ & \therefore \dfrac{a}{b}=\dfrac{+2\sin \left( \dfrac{\alpha +\beta }{2} \right)\sin \left( \dfrac{\alpha -\beta }{2} \right)}{2\cos \left( \dfrac{\alpha +\beta }{2} \right)\sin \left( \dfrac{\alpha -\beta }{2} \right)} \\\ \end{aligned}$$ Cancel out $$\sin \left( \dfrac{\alpha -\beta }{2} \right)$$ from numerator and denominator. $$\therefore \dfrac{a}{b}=\dfrac{+\sin \left( \dfrac{\alpha +\beta }{2} \right)}{\cos \left( \dfrac{\alpha +\beta }{2} \right)}$$ We know that, $$\dfrac{\sin \theta }{\cos \theta }=\tan \theta $$. $$\begin{aligned} & \therefore \dfrac{a}{b}=\tan \left( \dfrac{\alpha +\beta }{2} \right) \\\ & \therefore a=b\tan \left( \dfrac{\alpha +\beta }{2} \right) \\\ \end{aligned}$$ Hence proved **Note:** We have used basic trigonometric identities. You can lease the answer as $$\left[ \dfrac{a}{b}=\dfrac{\cos \beta -\cos \alpha }{\sin \alpha -\sin \beta } \right]$$ also but further simplify it to get the expression as mentioned in the question. Remember the trigonometric identities. Another approach is to directly find $$\tan \alpha $$ and $$\tan \beta $$, then use the formula, $$\tan \left( \alpha +\beta \right)=\dfrac{\left( \tan \alpha +\tan \beta \right)}{\left( 1+\tan \alpha .\tan \beta \right)}$$. Try not to make any calculation mistakes while solving the question.