Question
Question: A resistance of \(R\Omega \)draws current from a potentiometer. The potentiometer wire, \(AB\), has ...
A resistance of RΩdraws current from a potentiometer. The potentiometer wire, AB, has total resistance of R0Ω.. A voltage V is supplied to the potentiometer. Derive an expression for the voltage across Rwhen the sliding contact is in the middle of the potentiometer wire.
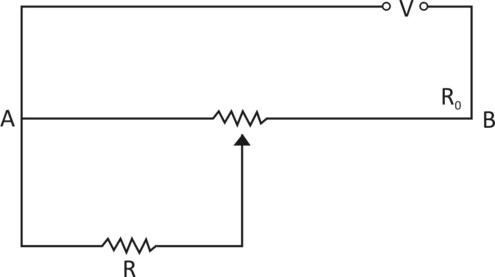
Solution
Concept of principle of potentiometer . As length increases, the potential drop across the length also increases and vice versa.
Complete step by step answer:
Potentiometer: It is a device that is used to measure unknown emf or potential differences.
Principle of potentiometer: It is based on the principle that when a constant current flows through a wire of uniform composition and cross-sectional area, then the potential drop across any length of wire will be directly proportional to that length as we know that, from ohm’s law
V=IR
And R=ρAℓ
So, V=AIρℓ
When V is the potential difference ρis the resistivity of wire A is the area of cross-section.
l is length of wire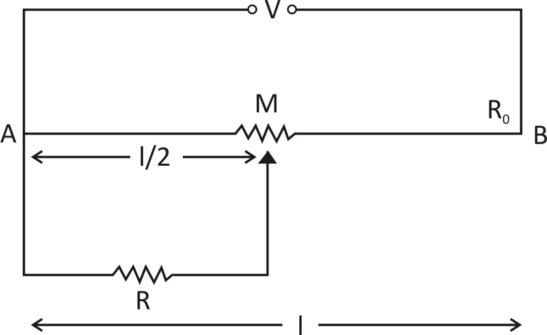
R is the resistance
Now, for uniform cross section and area and constant current
ATP=constant=K(let)
So, V=kℓ
Vαℓ
Which is the basic principle of potentiometer or we can also say potential gradient that is variation of potential with length his constant
⇒ℓV=constant=K
Now, in the question, let the length of wire be ℓ.
And Mbe the mid point of wire.
Now, if Vis the potential applied between A and B points then, according to principle of potentiometer
Vαℓ
V=kℓ …..(i)
Where kis constant.
Let voltage across RbeV′and is equal to AM where length is μ2so,
V′α2ℓ
⇒V′=2Kℓ ……(ii)
From (i) and (ii) we get,
V′=2V
Note:
As the potential difference depends on the end point so the potential drop across resistor R will be the same as V' which is in accordance with the principle of potentiometer.
