Question

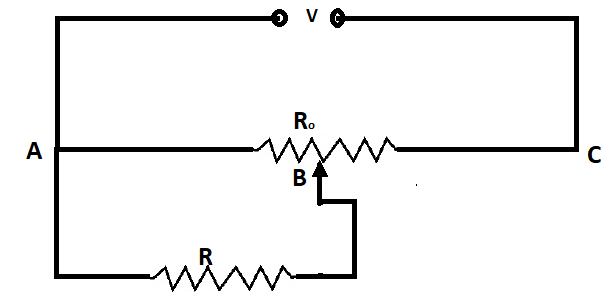
A resistance of $R \Omega$ draws current from a potentiometer as shown in the figure. The potentiometer has a total resistance $R_0 \Omega$. A voltage $V$ is supplied to the potentiometer. Derive an expression for the voltage across R when the sliding contact is in the middle of the potentiometer.

Answer 1

A potentiometer circuit is called balanced when the voltage drop across the sliding resistance is equal to the resistance of the wire it traversed. In this the voltage drop across the length of the wire the slider traversed will be equal to the voltage drop across the slider i.e both will be in parallel connection.

Complete step by step solution:
Here in this question, it is given that the resistance r drives current from the potentiometer
And we need to derive an equation for voltage Across when the sliding contact is at the center i.e. at B .
Now, Here it is given that we have to derive the equation when the contact is in the middle so we can say that $AB = \dfrac{{AC}}{2}$.
Now as we know that resistance of a wire depends upon length and area
$R \propto \dfrac{L}{A}$
To remove the constant of proportionality we introduce $\rho$ which is called resistivity and is the property of the wire material
So the equation becomes, $R = \dfrac{{\rho L}}{A}$
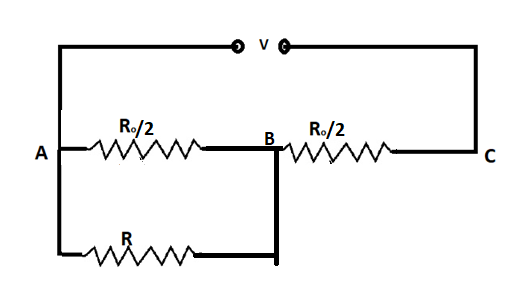
Here we can see that the resistance of the wire is directly proportional to the length and in this case we are reducing the wire length ${R_0}$ by half
So resistance ${R_{ab}} = \dfrac{{{R_0}}}{2}$
Now our circuit looks like

As here we can see that
Current $I$ is flowing from the source then at it is divided into ${I_1}$ and ${I_2}$
Now ${I_1}$ flows across $\dfrac{{{R_0}}}{2}$
And ${I_2}$ flows across $R$
Not at B both streams join each other and current${I_1}$ and ${I_2}$ re-joins and flows through the resistance ${R_{BC}}$

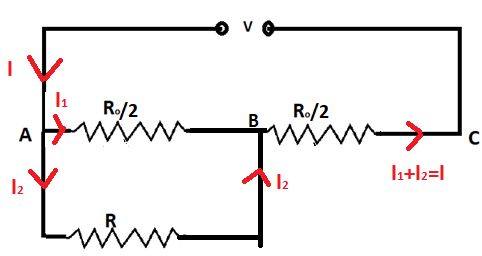
From here we can conclude that since the current is dividing between ${R_{AB}}$and R hence they are parallel to each other and their equivalent resistance will be in series connection with ${R_{BC}}$
Equivalent resistance when resistances are in parallel connection is given by
$\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}$
So here it will be
$\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{\dfrac{{{R_0}}}{2}}} + \dfrac{1}{R}$
$\Rightarrow {R_{eq}} = \dfrac{{{R_0}R}}{{2R + {R_0}}}$(1)
Now our circuit looks like

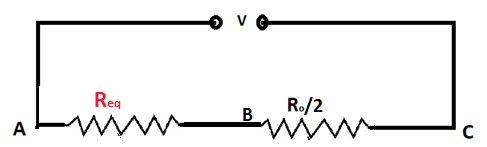
Now we will again find equivalent resistance for the remaining circuit
As we can see that this resistance are in series connection and equivalent resistance in series is given by
${R_s} = {R_{eq}} + {R_{BC}}$
Substituting values we get
${R_s} = \dfrac{{{R_0}R}}{{2R + {R_0}}} + \dfrac{{{R_0}}}{2}$
$\Rightarrow {R_s} = {R_0}\left[ {\dfrac{{2R + 2R + {R_0}}}{{2\left( {2R + {R_0}} \right)}}} \right]$
$\Rightarrow {R_S} = \dfrac{{{R_0}}}{2} \times \dfrac{{\left( {{R_0} + 4R} \right)}}{{\left( {{R_0} + 2R} \right)}}$
So our equivalent resistance will be ${R_S} = \dfrac{{{R_0}}}{2} \times \dfrac{{\left( {{R_0} + 4R} \right)}}{{\left( {{R_0} + 2R} \right)}}$
This resistance will be for the whole circuit
Now we have got our equivalent resistance
Apply ohm's law on the circuit
$V = I{R_s}$
Substituting the value of resistance we get
$V = I \times \left[ {\dfrac{{{R_0}}}{2} \times \dfrac{{\left( {{R_0} + 4R} \right)}}{{\left( {{R_0} + 2R} \right)}}} \right]$
$\Rightarrow I = \dfrac{{2V\left( {{R_0} + 2R} \right)}}{{{R_0}\left( {{R_0} + 4R} \right)}}$_________(2)
Now we need to drive expression for voltage across R
Let the voltage across R be ${V_1}$
Since ${R_{AB}}$ and R are in parallel so the voltage across them will be the same
So as we know that if the potentiometer needs to be balanced the voltage across AB should be equal to the voltage drop across R
So we will apply ohm's law here also
Applying Ohm's law to the equivalent resistance of ${R_{AB}}$ and R we get
$\because V = IR$
here substituting the value of R as ${R_{eq}}$
Substituting value I from equation 2 and value of ${R_{eq}}$from equation 1 we get
${V_1} = \dfrac{{2V\left( {{R_0} + 2R} \right)}}{{{R_0}\left( {{R_0} + 4R} \right)}} \times \dfrac{{{R_0}R}}{{2R + {R_0}}}$
$\Rightarrow {V_1} = \dfrac{{2VR}}{{{R_0} + 4R}}$

The voltage drop across the slider resistance R will be $\dfrac{{2VR}}{{{R_0} + 4R}}$.

Note: When current gets divided into two branches it implies that they are in parallel connection. In a parallel connection, the voltage across the joined resistance remains the same. When current passes through resistances added without getting divided then resistances are in series connection in this case the voltage gets divided.