Question

A resistance of $9\Omega$ is connected to the terminal of a cell. A voltmeter connected across the cell reads is 1.8 volt. When the resistance of $10\Omega$ is connected in series with $9\Omega$ the voltmeter reading changes to 1.9V. Calculate the emf of the cell and its internal resistance.

Answer 1

Ohm’s law states that the current in the circuit is directly proportional to the potential difference across the circuit. Use the ohm’s law to find the current that is V = IR. After that find the emf of the cell and internal resistance by using the relation between emf and current.
Formula used:
To calculate current use the formula V = IR and to find emf using formula of emf
$I=\dfrac{E}{R+r}$

Complete answer:
In order to understand the question properly and then the solve for the required answer, first create an electrical circuit diagram of the given system. The given system in both its possible cases can be represented by the following electrical diagram:

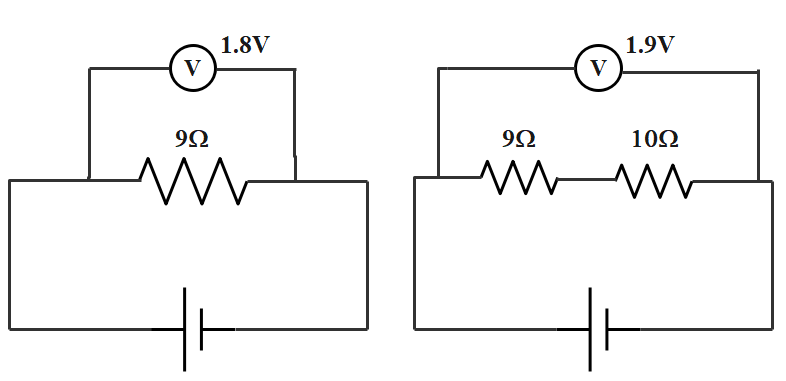
We wish to find the internal emf of the cell and the emf provided by it. Let us start with the first electrical circuit. So,
Let us suppose ${{R}_{1}}=9\Omega, {{V}_{1}}=1.8V$ according to the ohm’s law
${{V}_{1}}={{I}_{1}}{{R}_{1}}$
Where, ${{V}_{1}}$ is the voltage, ${{I}_{1}}$ is current and ${{R}_{1}}$ is the resistance in the circuit. By putting above values of ${{V}_{1}}\text{and}{{R}_{1}}$ we get,
$\begin{aligned} & \Rightarrow 1.8={{I}_{1}}\times 9 \\\ & \Rightarrow {{I}_{1}}=\dfrac{1.8}{9} \\\ & \Rightarrow {{I}_{1}}=0.2A \\\ \end{aligned}$
As we know that, ${{I}_{1}}=\dfrac{E}{({{R}_{1}}+r)}$
Put the values of ${{I}_{1}}\text{and}{{R}_{1}}$
$\begin{aligned} & \Rightarrow 0.2=\dfrac{E}{\left( 9+r \right)} \\\ & \Rightarrow E=0.2\left( 9+r \right).......(1) \\\ \end{aligned}$
In second situation suppose
${{R}_{2}}=10\Omega, {{V}_{2}}=1.9V,R'={{R}_{1}}+{{R}_{2}}=19\Omega$
Similarly using ohm’s law
${{V}_{2}}={{I}_{2}}R'$
Where, ${{V}_{2}}$ is voltage, ${{I}_{2}}$ is current and R’ is the resistance in the second circuit.
$\begin{aligned} & \Rightarrow 1.9={{I}_{2}}\times 19 \\\ & \Rightarrow {{I}_{2}}=\dfrac{1.9}{19} \\\ & \Rightarrow {{I}_{2}}=0.1A \\\ \end{aligned}$
As we know that, ${{I}_{2}}=\dfrac{E}{(R'+r)}$
Put the values of ${{I}_{2}}$and R’
$\begin{aligned} & \Rightarrow 0.1=\dfrac{E}{\left( 19+r \right)} \\\ & \Rightarrow E=0.1\left( 19+r \right).....(2) \\\ \end{aligned}$
From (1) and (2) we get
$\begin{aligned} & \Rightarrow 0.2(9+r)=0.1\left( 19+r \right) \\\ & \Rightarrow 1.8+0.2r=1.9+0.1r \\\ & \Rightarrow 0.2r-0.1r=1.9-1.8 \\\ & \Rightarrow 0.1r=0.1 \\\ & \Rightarrow r=1\Omega \\\ \end{aligned}$
This is the internal resistance of the cell. Now, to calculate emf of cell put the values of r in equation (1)
$\begin{aligned} & \Rightarrow E=0.2(9+1) \\\ & \Rightarrow E=0.2\left( 10 \right) \\\ & \Rightarrow E=2V \\\ \end{aligned}$
Which is the emf of the cell hence, emf of the cell is 2V and internal resistance is 1Ω.

Note:
It is advised to remember the ohm’s law according to which voltage is directly proportional to the current in the circuit. It is compulsory to write the units of current, emf, resistance and voltage. Additionally, note that voltmeter is always connected in parallel to the circuit because potential remains constant in parallel connection.