Question

A resistance of $300\Omega$ and an inductance of $\dfrac{1}{\pi }$ henry are connected in series to an A.C. voltage of $20 volts$ and $200Hz$ frequency. The phase angle between the voltage and current is:-
A. ${\tan ^{ - 1}}\left( {\dfrac{4}{3}} \right)$
B. ${\tan ^{ - 1}}\left( {\dfrac{3}{4}} \right)$
C. ${\tan ^{ - 1}}\left( {\dfrac{3}{2}} \right)$
D. ${\tan ^{ - 1}}\left( {\dfrac{2}{3}} \right)$

Answer 1

When an AC flows through a resistor, the voltage and current are in phase. The phase angle of a circuit depends on the phase difference between voltage and current. If the value of resistors, inductors, and capacitors is known, the phase angle between the voltage and current can be determined. Also, using the time difference between current and voltage waveform phase angle can be determined.

Formula used:
To calculate the phase angle between the voltage and the current, depending on the given data we can use, $\tan \phi = \dfrac{{{V_L}}}{{{V_R}}}$

Complete step by step solution:
According to the problem resistance $R = 300\Omega$, induction $L = \dfrac{1}{\pi }hrnry$. Now, the resistance and induction are both connected in a series.
Let, the phase angle between the voltage and current is $\phi$ and angular frequency is $\omega$
And, frequency is $f = 200Hz$
Therefore, \omega = 2\pi f$$$$ = 2\pi \times 200$$$$ = 400\pi

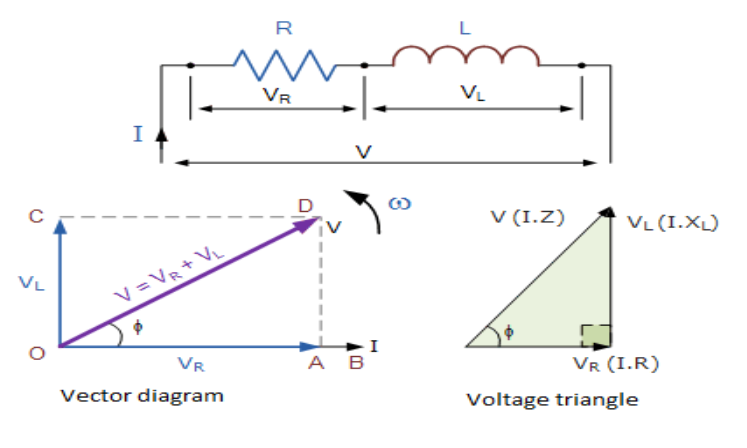
The two-component voltages are ${V_L}$and ${V_R}$
As we know, $\tan \phi = \dfrac{{{V_L}}}{{{V_R}}}$
\Rightarrow \tan \phi = \dfrac{{I\omega L}}{{IR}}$$$$ = \dfrac{{400\pi \times \dfrac{1}{\pi }}}{{300}}$$$$ = \dfrac{4}{3}

Note:
The phase difference is $\leqslant {90^ \circ }$. Phase relates a full cycle or period to ${360^ \circ }$ as a reference.
The power delivery by AC depends on its phase angle between voltage and current.
The real power delivery load can be low because of the phase difference between voltage and current. To ensure real power delivery to a resistive load, the power factor of the circuit need to be high thus, the phase angle need to be near zero
The phase angle depends on the impedance of the circuit.