Question

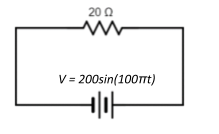
A resistance of $20\Omega$ is connected to a source of an alternating potential $V=200sin(100\pi t)$. The time taken by the current to change from its peak value to r.m.s value is:

A. $0.2\;s$
B. $0.25\;s$
C. $25\times 10^{-3}\;s$
D. $2.5\times 10^{-3}\;s$

Answer 1

Using Ohm’s law determine the expression for instantaneous current by using the alternating potential and resistance value given to us. We know that the rms current is essentially the instantaneous current sampled multiple times over an interval of time. We also know that the rms current can be expressed in terms of the peak current. Equate the above two expressions for rms current, to arrive at an arithmetically evaluable form for the time the current takes to change from its peak value to a near average value.

Formula Used:
$I_{rms} = I(t) = I_0sin(\omega t)$
$I_{rms}= \dfrac{I_0}{\sqrt{2}}$

Complete Step-by-Step Solution:
Let us begin by understanding the terms alternating potential, peak current and rms current.
An alternating potential is the voltage whose magnitude and direction change with time, and attains the same magnitude and direction in definite time intervals.
An alternating potential in a circuit produces an alternating current (AC) flowing through the circuit, whose magnitude changes with time and direction reverses periodically.
The value of current or voltage in an AC circuit at any instant of time is called the instantaneous value and is given respectively as:
$I(t) = I_0sin(\omega t)$ and $V(t)=V_0sin(\omega t)$,
where $I_0$ and $V_0$ are the peak current and peak voltage, $\omega$ is the angular frequency that defines the sinusoidal variation of current and voltage with time t.

The maximum value that the current can reach in an AC circuit is called as the peak current. It is also known as the crest value, or amplitude. It is usually denoted as $I_0$.
The rms or root means the square value of an AC is defined as that steady current which produces the same amount of heat in a circuit in a certain time interval as produced by the AC in the same conductor in the same time interval. It is denoted by $I_{rms}$ and is given as:
$I_{rms} = \dfrac{I_0}{\sqrt{2}}$
Now, using this information at hand, let us look at the problem given to us.
We are given an alternating potential $V=200sin(100\pi t)$ across which is connected to a resistance of $20\;\Omega$. Using Ohm’s Law, we can deduce the alternating current as follows:
Ohm’s law $V(t)=\dfrac{I(t)}{R} \Rightarrow I(t)= \dfrac{V(t)}{R} = \dfrac{200sin(100\pi t)}{20}$
$\Rightarrow I(t)= 10sin(100\pi t)$
The above expression is in the form $I(t) = I_0sin(\omega t)$. This means that the value of peak current $I_0 = 10\;A$
Now, since rms values of current are based on time and are calculated by taking many samples of instantaneous values of current, we can write:
$I_{rms} = I(t) = 10sin(100\pi t)$
But we also know that $I_{rms} = \dfrac{I_0}{\sqrt{2}} = \dfrac{10}{\sqrt{2}}$

By equating the previous two expressions we can find the time t taken by the current to change from its rms to peak value:
$10sin(100\pi t) = \dfrac{10}{\sqrt{2}}$
$\Rightarrow 100\pi t = sin^{-1}\left(\dfrac{1}{\sqrt{2}}\right)$
We know that $sin(\dfrac{\pi}{4}) = \dfrac{1}{\sqrt{2}}$
$\Rightarrow 100\pi t = \dfrac{\pi}{4}$
$\Rightarrow t = \dfrac{1}{4\times 100} = 0.25 \times 10^{-2} = 2.5 \times 10^{-3}\;s$

Therefore, the correct choice would be D. $2.5 \times 10^{-3}\;s$.

Note:
It is a common misconception to interchangeably use rms current and average current. Though we can heuristically understand the rms current to be the average since it is obtained by sampling multiple instantaneous current values, it is not necessarily true when looked at from a statistical point of view. RMS stands for the root-mean-square of instantaneous current values, i.e., for a set of n instantaneous current values,
$I_{rms} = \sqrt{\dfrac{1}{n}(I_1^2 + I_2^2 + ….. + I_n^2)}$
Whereas, $I_{average} = \dfrac{1}{n}(I_1 + I_2 +….. +I_n)$
Thus, it becomes important to distinguish between the two, should the problem demand the same.