Question

A regular octagon is inscribed in a circle of radius $1m$. Find the side of the octagon.

Answer 1

Try to work separately on one of the eight triangles made from joining the vertices with the centre. Construct a perpendicular from a vertex to side and find out the required length using Pythagoras’ theorem.

Complete step-by-step answer:

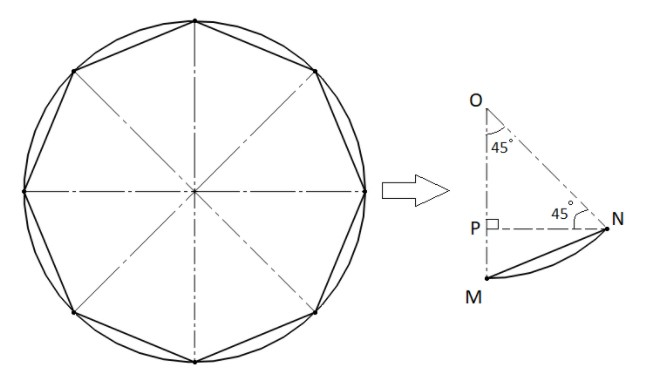
Let us first draw a figure to solve this problem. Remember in a regular octagon, there are 8 sides of equal length and with equal interior angles.
Now just join all the vertices of the octagon to the centre of the circle, which in this case also the centre of the polygon. This should look like the above-shown figure with eight equal sectors.
Since all the sides are equal and the polygon is inscribed in the circle, the angle subtended by each of these sides will also be equal.
We know that a whole angle is $360^\circ$. So, that makes each of the angles subtended my side of the octagon $= \dfrac{{360}}{8} = 45^\circ$
For the ease of our understanding, just imagine one of the eight pieces of the circle separately as shown in the figure. Name it as the sector $MON$ , which also has $\Delta MON$ and an arc $MN$ in it.
So, now we need to find the length of the side $MN$ and we already know that $OM = ON = 1m$ as they are the radius of the circle and $\angle MON = 45^\circ$
Now make a perpendicular $NP$ from N to the radius $OM$.
Since, the sum of all the angles in a triangle$= 180^\circ$, we get: $\angle ONP = 180^\circ - \angle PON - \angle NPO = 180^\circ - 45^\circ - 90^\circ = 45^\circ$
Also, we know that in a triangle, sides opposite to equal angles are also equal. This will give us a relation$\equiv \angle ONP = \angle NOP \Rightarrow OP = NP$
Using Pythagoras’ theorem in $\Delta NOP$ which states that “In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides“, we get:
$O{N^2} = N{P^2} + O{P^2} \Rightarrow O{N^2} = 2 \times N{P^2} \Rightarrow N{P^2} = \dfrac{1}{2} \Rightarrow NP = \dfrac{1}{{\sqrt 2 }}$
And since the radius $OM = 1$; $PM = OM - OP = 1 - \dfrac{1}{{\sqrt 2 }}$
Now we will again use Pythagoras’ theorem in $\Delta NPM$ , which will be as:
$M{N^2} = P{M^2} + N{P^2} = {\left( {1 - \dfrac{1}{{\sqrt 2 }}} \right)^2} + {\left( {\dfrac{1}{{\sqrt 2 }}} \right)^2}$
Let’s expand this using ${\left( {a - b} \right)^2} = {a^2} - 2ab + {b^2}$ and find the value of $MN$
$M{N^2} = 1 - 2 \times \dfrac{1}{{\sqrt 2 }} + \dfrac{1}{2} + \dfrac{1}{2} = 1 - \sqrt 2 + 1 = 2 - \sqrt 2$
$MN = \sqrt {\left( {2 - \sqrt 2 } \right)} \approx \sqrt {2 - 1.414} \approx 0.765m$
So, the length of each side of the octagon is $\sqrt {\left( {2 - \sqrt 2 } \right)} \approx 0.765m$

Note: Be careful while calculating square roots in Pythagoras’ theorem use braces if needed. An alternative approach is to use trigonometric terms like Sine, Cosine etc. instead of Pythagoras theorem.Another alternative method is there where you can work easily by drawing perpendicular from O to $MN$ and then using Pythagoras’ theorem.