Question

A regular hexagon of side $10 cm$ has a charge $5μC$ at each of its vertices. Calculate the potential at the centre of the hexagon.

Answer 1

A hexagon is a regular figure having six sides. At each corner 6 charges are placed and we need to find the potential at the centre of the regular hexagon. We know electric potential is a scalar quantity, so we do not have concern about the direction. Since, the distance of all the charges is the same so we just find out potential due to a single charge and then multiply it by 6.

Complete step by step answer:

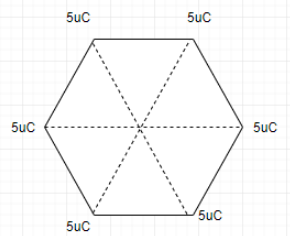
when all the corners are joined to the centre of the hexagon, it forms an equilateral triangle. So, the distance between the centre to any of the corner is 10 cm = 0.1 m.We know electric potential is given by the formula:
$V=k\dfrac{Q}{r}$,
where Q is the charge and r is the distance between the charge and the point where the potential is to be determined and k is a constant whose value is $k=9\times {{10}^{9}}N{{m}^{2}}/{{C}^{2}}$.
Given, $Q=5\mu C=5\times {{10}^{-6}}C$
V=k\dfrac{Q}{r} \\\ \Rightarrow V=\dfrac{9\times {{10}^{9}}\times 5\times {{10}^{-6}}}{0.1} \\\ \Rightarrow V=450000V \\\
For total 6 charges, $6\times 450000=2.7\times {{10}^{6}}V$

Hence, the potential at the centre of the hexagon is $2.7\times {{10}^{6}}V$.

Note: Electric potential is a scalar quantity and it is assumed to be zero at the infinity. If we want to move a charge from one point to another and if the electric potential is same at both the points work done will be zero because no work is required to be done to move a charge on an equipotential surface.The electric potential is related to electric field and electric field is defined as the negative gradient of electric potential.