Question

a) Region 1 had positive acceleration b) region 1 and 2 have positive acceleration c) Region 1 has negative acceleration d) Region 1 has negative and 2 has positive acceleration

• A. Region 1 had positive acceleration
• B. region 1 and 2 have positive acceleration
• C. Region 1 has negative acceleration
• D. Region 1 has negative and 2 has positive acceleration

Answer 1

Answer: (D)

Region 1 has negative and 2 has positive acceleration

Answer 2

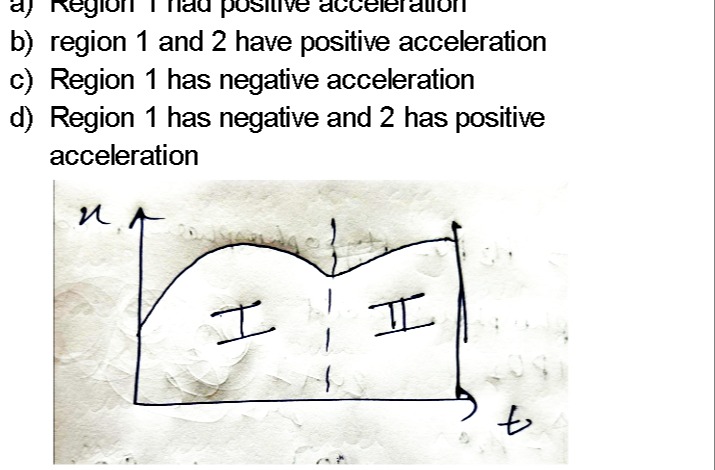
The given graph is a velocity-time (v-t) graph, where 'u' (presumably velocity) is on the y-axis and 't' (time) is on the x-axis. The acceleration 'a' is defined as the rate of change of velocity, which corresponds to the slope of the velocity-time graph:

$a = \frac{dv}{dt} = \text{slope of v-t graph}$

Let's analyze the acceleration in Region I and Region II based on the slope:

Analysis of Region I:

1. Initial part of Region I: The curve is rising, meaning the velocity is increasing. The slope of the graph in this part is positive. Therefore, the acceleration is positive.
2. Peak of Region I: At the peak, the velocity is maximum, and the slope of the graph is zero. Therefore, the acceleration is zero.
3. Latter part of Region I (after the peak): The curve is falling, meaning the velocity is decreasing. The slope of the graph in this part is negative. Therefore, the acceleration is negative.

So, Region I has both positive and negative acceleration.

Analysis of Region II:

1. Initial part of Region II (before the trough): The curve is falling, meaning the velocity is decreasing. The slope of the graph in this part is negative. Therefore, the acceleration is negative.
2. Trough of Region II: At the trough, the velocity is minimum, and the slope of the graph is zero. Therefore, the acceleration is zero.
3. Latter part of Region II (after the trough): The curve is rising, meaning the velocity is increasing. The slope of the graph in this part is positive. Therefore, the acceleration is positive.

So, Region II has both negative and positive acceleration.

Given that the options provide a single sign for acceleration for each region, it implies that we should consider the average acceleration over the region or the overall trend of velocity change.

Considering Average Acceleration:

Average acceleration ($\bar{a}$) over a time interval is given by:

$\bar{a} = \frac{\Delta v}{\Delta t} = \frac{v_{final} - v_{initial}}{t_{final} - t_{initial}}$

1. For Region I:

   • Observe the initial velocity ($v_{initial, I}$) at the start of Region I.
   • Observe the final velocity ($v_{final, I}$) at the end of Region I (at the dashed line).
   • From the graph, it appears that the final velocity in Region I is lower than the initial velocity ($v_{final, I} < v_{initial, I}$).
   • Therefore, $\Delta v = v_{final, I} - v_{initial, I}$ would be negative.
   • Since $\Delta t$ is positive, the average acceleration in Region I is negative.

2. For Region II:

   • Observe the initial velocity ($v_{initial, II}$) at the start of Region II (which is $v_{final, I}$).
   • Observe the final velocity ($v_{final, II}$) at the end of Region II.
   • From the graph, it appears that the final velocity in Region II is higher than the initial velocity ($v_{final, II} > v_{initial, II}$).
   • Therefore, $\Delta v = v_{final, II} - v_{initial, II}$ would be positive.
   • Since $\Delta t$ is positive, the average acceleration in Region II is positive.

Based on the interpretation of average acceleration, option (d) matches our analysis.

The final answer is d) Region 1 has negative and 2 has positive acceleration

Explanation of the solution:

The acceleration is the slope of the velocity-time graph. In Region I, the velocity first increases (positive slope, positive acceleration) and then decreases (negative slope, negative acceleration). However, the final velocity in Region I appears to be lower than the initial velocity. Thus, the overall change in velocity is negative, implying negative average acceleration. In Region II, the velocity first decreases (negative slope, negative acceleration) and then increases (positive slope, positive acceleration). The final velocity in Region II appears to be higher than the initial velocity of Region II. Thus, the overall change in velocity is positive, implying positive average acceleration. Therefore, Region 1 has negative acceleration (on average) and Region 2 has positive acceleration (on average).