Question

A rectangular wooden block $5cm \times 10cm \times 10cm$ in size is kept on a horizontal surface with its face of the largest area on the surface. A minimum force of $1.5N$ applied parallel to the surface sets the block in sliding motion along the surface. If the block is now kept with its face of smaller area in contact with the surface, the minimum force applied to the surface to set the block in motion is
$(A)$ Greater than $1.5N$
$(B)$Less than $1.5N$
$(C)$Equal to $1.5N$
$(D)$May be greater or less than $1.5N$

Answer 1

The force of friction comes from the surface characteristics of materials that came into contact. The normal force i.e., a force perpendicular to the surface of an object is sliding on, which relates to the friction force. The two forces are proportional hence the coefficient of friction can be used, and it’s something measured for the contact between two particular surfaces which can be related to an equation.

Complete answer:
We take a rectangular block of $5cm \times 10cm \times 10cm$ as shown

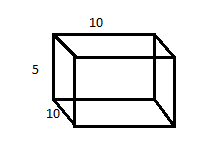
If the face of the largest area is kept on the horizontal surface then

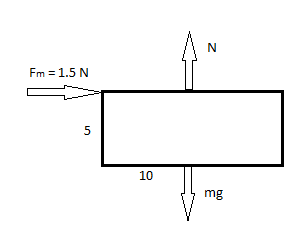
Initially, we take a force perpendicular to an object sliding and a frictional force that comes from the characteristics of the material. The frictional force is always independent of the area of contact when the minimum frictional force of $1.5N$ is applied to it
${F_{friction}} = \,{F_m} = \mu \times {F_{normal}}$ Where ${F_{normal}} = mg$
We get $\mu = \dfrac{{1.5}}{{mg}}$…….Equation (1)
Then we take the smaller area of the block in contact with the horizontal surface we get
The following equation relates the magnitude of the force of friction to the magnitude of the normal force. The normal force is always directed perpendicular to the surface, and the friction force is always directed parallel to the surface. ${F_l}$ And ${F_n}$are always perpendicular to each other. We get
${F_l} = \mu \times {F_n}$
From equation (1) we get
${F_l} = \dfrac{{1.5}}{{mg}} \times mg$
Therefore the minimum force applied parallel to the surface to set the block in motion is ${F_l} = 1.5N$(option C). Hence we can say that the force of friction is independent of the area of contact.

Note: Here we arrive at a conclusion where initially we take the larger area of contact for the frictional force to be applied. Then we take the $\mu$ value from the equation and use this constant to the smaller area of contact. We obtain the required minimum force to set the block in motion which proves that the frictional force is not dependent on the area of contact.