Question

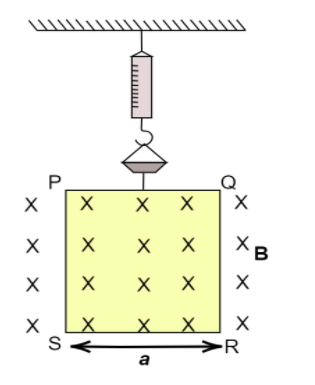
A rectangular wire loop of width $a$ is suspended from the insulated pan of a spring balance as shown in figure (34-E5). A current $i$ exists in the anticlockwise direction in the loop. A magnetic field $B$ exists in the lower region. Find the change in the tension of the spring if the current in the loop is reversed.

Answer 1

The force on a current-carrying loop due to a magnetic field is given by the current times the cross product of the magnetic field strength, the length of the wire (which has direction as the direction of current flow). When the direction of the current reverses, the direction of the force also changes.

Complete step by step answer:
For a current-carrying loop, the force experienced by it due to a magnetic field is given by the formula-
$F = i\left( {B \times L} \right)$
Where $i$ is the current flowing in the loop,
$B$ is the strength of the magnetic field,
And $L$ is the length of the wire,
The cross product indicates that the force depends on the orientation between the direction of the current and the magnetic field. It also implies that the direction of the force is given by the right-hand rule. That is, the force is perpendicular to the plane containing the magnetic field and current. If the fingers of the right hand are outstretched and the direction of the thumb in the direction of the current, the fingers face towards the magnetic field then the palm of the hand gives the direction of the force.
We know that the direction of the current in the loop is anticlockwise. The magnetic field is directed inwards and spans only in the lower part of the loop. Therefore, in the loop PQRS, the side PQ does not experience any force due to the magnetic field.
The sides, QR and PS also do not experience any force due to the magnetic field due to their orientation. This leaves only side RS that experiences a force.
According to the right-hand rule, the force can upward or downward. When the current is anticlockwise, an upward force acts on the side RS.
The length of the side RS is $a$. Then the magnitude of this force is-
${F_i} = Bia$ (in the upward direction, taking upwards positive).
When the current is reversed, the direction of this force changes, now it acts downwards which is denoted by a negative sign.
The magnitude of this force is-
${F_f} = - Bia$
The total movement of the spring is given by the difference in the initial and final readings-
$\Delta F = - Bia - Bia$
$\Delta F = - 2Bia$
The change in the tension of the spring is $2Bia$, and the net direction of motion of the spring balance is downwards.

Note: The forces due to the sides PS and QR are termed as zero because they are opposite in direction and get canceled out, resulting in only a net compressive or tensile force. These forces do not affect the reading of the spring balance as well so they are not included in the calculation.