Question

A rectangular tube of uniform cross section has three liquids of densities ${{\rho }_{1}}$,${{\rho }_{2}}$ and ${{\rho }_{3}}$. Each liquid column has length of sides of the equilateral triangle. Find the length x of the liquid of density ${{\rho }_{1}}$ in the horizontal limb of the tube, if the triangular tube is kept in the vertical plane.

Answer 1

The length of the tubes and the cross section are uniform so, the pressure at one end of the tube is equal to the other end at the base, so by equating pressure of both left and right side and by putting all the values of length, height of different liquids we will calculate our required answer.
Formula used:
Pressure P due to liquid is given by,
$\Rightarrow P=\rho gh$

Complete answer: :
When a liquid is placed in a column with some height at equilibrium it exerts a pressure due to force of gravity which is known as hydrostatic force.
The initial diagram according to the above problem statement is given by,

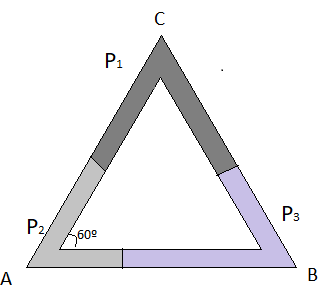
Now, by measuring heights and assuming length of liquid of density ${{\rho }_{1}}$ at base be x and length of side of triangle be $l$ so,

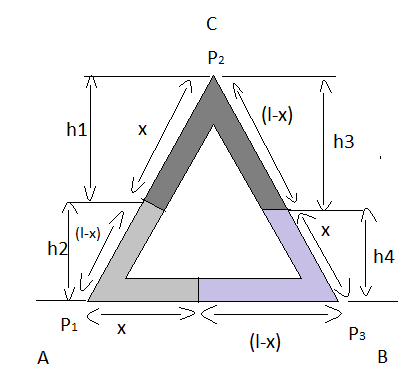
Given, P1 =${{\rho }_{1}}$(density of liquid one), P2=${{\rho }_{2}}$(density of liquid two) and P3=${{\rho }_{3}}$ (density of liquid three) from the above diagram,
Now, pressure at point A will be,
$\Rightarrow P=\rho gh$
$\Rightarrow {{P}_{A}}={{\rho }_{1}}g{{h}_{1}}+{{\rho }_{2}}g{{h}_{2}}$
$\Rightarrow {{h}_{1}}=x\cos {{30}^{\circ }}$
$\Rightarrow {{h}_{2}}=(l-x)\cos {{30}^{\circ }}$
$\Rightarrow {{P}_{A}}={{\rho }_{1}}g(l-x)\cos {{30}^{\circ }}+{{\rho }_{2}}gx\cos {{30}^{\circ }}.......(1)$
Similarly for pressure at point B will be,
$\Rightarrow {{P}_{B}}={{\rho }_{2}}g{{h}_{3}}+{{\rho }_{3}}g{{h}_{4}}$
$\Rightarrow {{h}_{3}}=(l-x)\cos {{30}^{\circ }}$
$\Rightarrow {{h}_{4}}=x\cos {{30}^{\circ }}$
$\Rightarrow {{P}_{B}}={{\rho }_{2}}g(l-x)\cos {{30}^{\circ }}+{{\rho }_{3}}gx\cos {{30}^{\circ }}........(2)$
Now by equating equation (1) and (2), we have
$\Rightarrow {{\rho }_{1}}g(l-x)\cos {{30}^{\circ }}+{{\rho }_{2}}gx\cos {{30}^{\circ }}={{\rho }_{2}}g(l-x)\cos {{30}^{\circ }}+{{\rho }_{3}}gx\cos {{30}^{\circ }}$
Value of g and $\cos {{30}^{\circ }}$will be cancel out from both side and the remaining equation is given by,
$\Rightarrow {{\rho }_{1}}(l-x)+{{\rho }_{2}}x={{\rho }_{2}}(l-x)+{{\rho }_{3}}x$
$\Rightarrow x{{\rho }_{2}}-x{{\rho }_{1}}+x{{\rho }_{2}}-x{{\rho }_{3}}=l{{\rho }_{2}}-l{{\rho }_{1}}$
$\Rightarrow x({{\rho }_{2}}-{{\rho }_{1}}+{{\rho }_{2}}-{{\rho }_{3}})=l({{\rho }_{2}}-{{\rho }_{1}})$
$\Rightarrow x=\dfrac{l({{\rho }_{2}}-{{\rho }_{1}})}{(2{{\rho }_{2}}-{{\rho }_{1}}+-{{\rho }_{3}})}$
$\therefore$ The length of liquid of density ${{\rho }_{1}}$at the base of the equilateral triangular tube will be given by,
$\Rightarrow x=\dfrac{l({{\rho }_{2}}-{{\rho }_{1}})}{(2{{\rho }_{2}}-{{\rho }_{1}}+-{{\rho }_{3}})}$

Note:
The pressure acting on a layer of fluid in bottom is directly proportional to the product of height and density of fluid and this pressure is mainly caused due to force of gravity. When density or height of fluid increases the pressure exerted at the bottom will increase. While increase in temperature of liquid will cause the molecules to separate and liquid will expand and density of liquid will decrease by which pressure exerted at bottom will decrease.