Question
Question: A rectangular tank of height \[10\,m\] filled with water, is placed near the bottom of a plane incli...
A rectangular tank of height 10m filled with water, is placed near the bottom of a plane inclined at an angle 30∘ with horizontal. At height h from the bottom a small hole is made (as shown in figure) such that the stream coming out from holestrikes the inclined plane normally. Calculate h
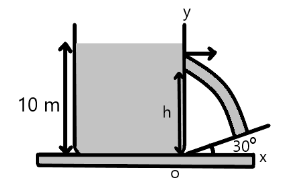
Solution
Here, we have to calculate the value of h, that is, the height at which the hole is made. For this, we will first calculate the time t at which the water stream strikes the inclined plane. The formula used for calculating the value time t is given below.
Formula used:
Here we will use the formula which is given below
v=u+at
Here, v is the final velocity, u is the initial velocity, a is the acceleration and t is the time taken.
Complete step by step answer:
According to the given question, the value of the velocity will be
v=2g(10−h)
Here, v is the velocity, g is the acceleration due to gravity and h is the height of the container.
Now, the component of the velocity parallel to the plane will be vcos30∘ and the component of the velocity perpendicular to the plane will be vsin30∘.When the stream strikes the plane after time t. Therefore, the formula of the velocity is given by
v=u+at
⇒0=vcos30∘−gt
⇒t=gsin30∘vcos30∘
⇒t=gvcot30∘
Now, the wave along the x-axis is represented by the following formula
x=vt
⇒x=gv2cot30∘=3y
⇒gv2cot30∘=3(h−21gt2)
⇒g3v2=3(h−21gt2)
⇒g3v2=3(h−21gg2v2cot230∘)
⇒gv2=(h−23gv2)
⇒h=gv2+2g3v2
⇒h=2g5v2
⇒h=2g5×2g(10−h)
⇒h=5(10−h)
⇒h+5h=50
⇒6h=50
∴h=8.33m
Therefore, the height h will be 8.33m.
Note: The value of the velocity v=2g(10−h) is of the water stream that is flowing out of the tank. Also, remember that here final velocity is not given, that is why, we have taken v=0. Also, vsin30∘ is the component of velocity in x-direction and sin30∘ is the component of velocity along y-direction.
