Question

A rectangular slab ABCD of refractive index ${\mu _1}$ is immersed in a liquid of refractive index ${\mu _2}$ $({\mu _2} < {\mu _1})$. A ray of light is incident on the surface AB of the slab as shown in the figure. The maximum value of incidence such that the ray comes out only from the surface CD is given by

A.${\sin ^{ - 1}}\left( {\dfrac{{\sqrt {{\mu _1}^2 - {\mu _2}^2} }}{{{\mu _2}}}} \right)$
B.${\sin ^{ - 1}}\left( {\dfrac{{\sqrt {{\mu _1}^2 - {\mu _2}^2} }}{{{\mu _1}}}} \right)$
C.${\sin ^{ - 1}}\left( {\dfrac{{{\mu _1}}}{{{\mu _2}}}} \right)$
D.${\sin ^{ - 1}}\left( {\dfrac{{{\mu _2}}}{{{\mu _1}}}} \right)$

Answer 1

At first draw a neat diagram showing the angles made by the ray. As the ray comes out through surface CD instead of surface AD, the ray suffers total internal reflection. Use the concept of total internal reflection to find out the maximum angle of incidence.

Complete Step by step answer: Given, refractive index of rectangular slab is ${\mu _1}$
Refractive index of liquid is ${\mu _2}$
First, we draw a neat diagram showing the angles of incidence, reflection and refraction.

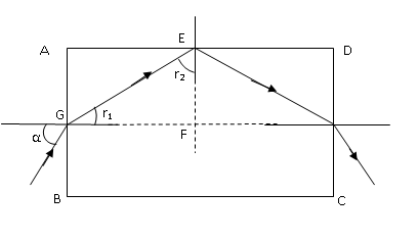
Let $\alpha$be the angle of incidence and ${r_1}$ be the angle of refraction on the surface AB.
As the ray the light incident on surface AB comes out of the surface CD, the ray must make total internal reflection at the surface AD as shown in the above figure.
Let ${r_2}$ be the angle of reflection at the surface AD.
From the figure we can see $\vartriangle {\text{EFG}}$ is a right angled triangle and $\angle F$ is a right angle, so we can write, ${r_1} + {r_2} = {90^ \circ }$
$\Rightarrow {r_1} = {90^ \circ } - {r_2}$ (i)

For total internal reflection on surface ED, the condition for total internal reflection must be satisfied which is, $\sin {\theta _C} = \dfrac{{{\mu _2}}}{{{\mu _1}}}$ where ${\theta _C}$ is the minimum angle of incidence for total internal reflection and
${\mu _1}$ is the refractive index of the rectangular slab and ${\mu _2}$ is the refractive index of liquid.
Here ${\theta _C} = {\left( {{r_2}} \right)_{\min }}$
$\therefore \sin {\left( {{r_2}} \right)_{\min }} = \dfrac{{{\mu _2}}}{{{\mu _1}}}$ (ii)
According to Snell’s law we have, ${n_1}\sin i = {n_2}\sin r$ where ${n_1}$ is the refractive index of incident medium, ${n_2}$ is the refractive index of refractive medium, $i$ is the angle of incidence and $r$ is the angle of refraction.
Now, applying Snell’s law at surface AB, we get
${\mu _2}\sin \alpha = {\mu _1}\sin {r_1}$
$\Rightarrow \sin \alpha = \dfrac{{{\mu _1}}}{{{\mu _2}}}\sin {r_1}$
Putting the value of ${r_1}$ from equation (i), we get

$$\Rightarrow \sin \alpha = \dfrac{{{\mu _1}}}{{{\mu _2}}}\cos {r_2} \\\$$

In the above equation, we can see that for angle of incidence $\alpha$ to be maximum, ${r_2}$ should be minimum that is,
$\sin {\alpha _{\max }} = \dfrac{{{\mu _1}}}{{{\mu _2}}}\cos {\left( {{r_2}} \right)_{\min }}$
$\Rightarrow \sin {\alpha _{\max }} = \dfrac{{{\mu _1}}}{{{\mu _2}}}\sqrt {1 - {{\sin }^2}{{\left( {{r_2}} \right)}_{\min }}}$
Now, we put the value of ${\left( {{r_2}} \right)_{\min }}$ and we have,

$$\sin {\alpha _{\max }} = \dfrac{{{\mu _1}}}{{{\mu _2}}}\sqrt {1 - {{\left( {\dfrac{{{\mu _2}}}{{{\mu _1}}}} \right)}^2}} \\\ \Rightarrow \sin {\alpha _{\max }} = \dfrac{{{\mu _1}}}{{{\mu _2}}}\sqrt {\dfrac{{{\mu _1}^2 - {\mu _2}^2}}{{{\mu _1}^2}}} \\\ \Rightarrow \sin {\alpha _{\max }} = \dfrac{{\sqrt {{\mu _1}^2 - {\mu _2}^2} }}{{{\mu _2}}} \\\ \Rightarrow {\alpha _{\max }} = {\sin ^{ - 1}}\left( {\dfrac{{\sqrt {{\mu _1}^2 - {\mu _2}^2} }}{{{\mu _2}}}} \right) \\\$$

Therefore the maximum value of angle of incidence for which the ray incident on surface AB comes out of surface CD is, ${\alpha _{\max }} = {\sin ^{ - 1}}\left( {\dfrac{{\sqrt {{\mu _1}^2 - {\mu _2}^2} }}{{{\mu _2}}}} \right)$
Hence, the correct answer is option (A) ${\sin ^{ - 1}}\left( {\dfrac{{\sqrt {{\mu _1}^2 - {\mu _2}^2} }}{{{\mu _2}}}} \right)$.

Note: Always draw a diagram in such type of questions showing all the angles made by the ray and look for the type of reflection made by the ray. And always remember total internal reflection occurs when the ray travels from denser to rarer medium and when the ray travels from rarer to denser medium a part of the ray is reflected and other part is refracted.