Question

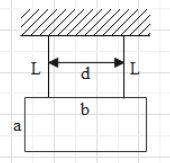
A rectangular plate of sides a and b are suspended from a ceiling by two parallel strings of length L each. The separation between the strings is d. The plate is displaced slightly in its plane keeping the strings tight. Show that it will execute simple harmonic motion. Find the time period.

Answer 1

Here we have given a setup in which a rectangular plate is attached to the ceiling with the help of two parallel strings of same length L which are separated by distance d. We have to prove that it executes simple harmonic motion and we have to find the time period for the oscillation. So first we will prove that it executes simple harmonic motion (SHM) and then by using the formula of time period for SHM we can get the time period.
Formula used:

& F=ma \\\ & T=\sqrt{\dfrac{d}{a}} \\\ \end{aligned}$$ **Complete step by step answer:** In the given diagram, the rectangular plate of sides a and b are suspended by two strings of equal length which are d distance apart. Now if we consider the center of mass of the rectangular plate, then the given diagram can be given as  Here we have assumed that mass of the rectangular plate is m and consider that the string is attached at the center of the plate i.e. taking center of mass. Now the length will be the same as if the two strings had the same length L. The equivalent diagram resembles a simple pendulum. Now when it is slightly displaced then it will have oscillatory motion. And the diagram will be given as  Here we have taken a shape of bob instead of block or plate for convenience. Now when the plate is displaced it will have some force which will be in the direction shown by F. And it is balanced by the sine component of mg. Also due to displacement it makes an angle θ with respect to the initial position. Hence we can write $$F=mg\sin \theta $$ Now we now that force is given as mass times acceleration, i.e. $$\begin{aligned} & F=ma \\\ & \Rightarrow a=\dfrac{F}{m} \\\ \end{aligned}$$ Here we got the acceleration. Now if we substitute the value of F from above equation for the plate we get acceleration for the simple pendulum $$\begin{aligned} & a=\dfrac{mg\sin \theta }{m} \\\ & \Rightarrow a=g\sin \theta \\\ \end{aligned}$$ Now we have given in question that it is displaced slightly, therefore θ will be small. For a small value of θ, sin θ is equal to θ. Hence we can write the acceleration term as $$a=g\theta \text{ }.......\text{(i)}$$ Now considering the triangle as shown below  Value of sine and cosine of θ will be given as $$\begin{aligned} & \sin \theta =\dfrac{x}{h} \\\ & \cos \theta =\dfrac{L}{h} \\\ \end{aligned}$$ Where h represents the hypotenuse. Now as the angle is very small therefore cosine of θ will be equal to one, and so we can write $$\begin{aligned} & \cos \theta =\dfrac{L}{h} \\\ & \Rightarrow \dfrac{L}{h}=1 \\\ & \Rightarrow L=h \\\ \end{aligned}$$ As it is small angle therefore sin θ is equal to θ, substituting value of h we get $$\begin{aligned} & \sin \theta =\dfrac{x}{h} \\\ & \Rightarrow \theta =\dfrac{x}{h} \\\ & \Rightarrow \theta =\dfrac{x}{L} \\\ \end{aligned}$$ Substituting above value of θ in equation (i), we get $$a=g\dfrac{x}{L}$$ In simple harmonic motion acceleration is directly proportional to x and from the above equation we can see that a is proportional to x, therefore the system will execute SHM. Now time period for the system can be given as $$T=\sqrt{\dfrac{x}{a}}$$ where x is displacement and a is acceleration. Substituting value of acceleration we calculated above we get $$\begin{aligned} & T=\sqrt{\dfrac{x}{\left( g\dfrac{x}{L} \right)}} \\\ & \Rightarrow T=\sqrt{\dfrac{L}{g}} \\\ \end{aligned}$$ Hence we got the time period for oscillation in terms of acceleration due to gravity and length of string. **Note:** It is not necessary that all oscillatory motions are simple harmonic motion. Although all simple harmonic motion is oscillatory motion. Here if there was a term of x i.e. displacement then we can convert it in other terms which are provided in the question. In case the length of the two strings were different then the setup cannot be considered as a simple pendulum.